Mathematics
Categories
ContactWarped Products and Conformal Rescalings
Conventions
In case there's any confusion, the following computations belong to a setting where
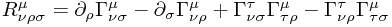
and of course
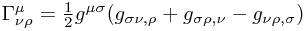
Warped Procucts
Suppose you have a space with coordinates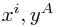 
of the form
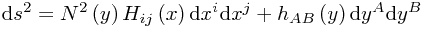
so that schematically
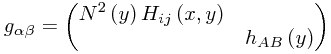
This is a so-called warped product. A common question is "What is the form of the Ricci tensor?"
Let the dimension of the x subspace - that is to say, how many values i can range over - be denoted by D. Then one obtains the result
![\begin{eqnarray*}
R_{AB} & = & \hat{R}_{AB}-D\frac{\nabla_{A}\nabla_{B}N}{N}\\
R_{ij} & = & \tilde{R}_{ij}-H_{ij}\left[N\Delta N+\left(D-1\right)h^{AB}\nabla_{A}N\cdot\nabla_{B}N\right]\\
R_{Ai} & = & 0
\end{eqnarray*}](/_static/latex/efa16e257f4c9b9e5aee6c1782510119.gif "\begin{eqnarray*}
R_{AB} & = & \hat{R}_{AB}-D\frac{\nabla_{A}\nabla_{B}N}{N}\\
R_{ij} & = & \tilde{R}_{ij}-H_{ij}\left[N\Delta N+\left(D-1\right)h^{AB}\nabla_{A}N\cdot\nabla_{B}N\right]\\
R_{Ai} & = & 0
\end{eqnarray*}")
where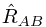 
is the Ricci tensor of the metric 
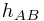and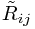 
is the Ricci tensor of the metric 
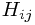. Note that 
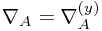is the covariant derivative with respect to the 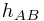metric.
Observe that the form of the modification to 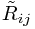is a multiple of the metric tensor for the x subspace.
Conformal Rescalings
Another very common computation involves the rescaling
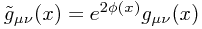
A direct computation in local inertial coordinates for the new metric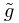 
gives the result
![\begin{eqnarray*}
\tilde{R}_{\nu\sigma} & = & R_{\nu\sigma}+(2-D)\left[ \nabla_\nu\nabla_\sigma \phi - \nabla_\nu \phi \nabla_\sigma \phi \right] \\
& & - g_{\nu\sigma} \left[ \nabla^\mu \nabla_\mu \phi + (D-2) \nabla_\mu \phi \nabla^\mu \phi \right] \\
\tilde{R} & = & R+2(1-D)\nabla^{2}\phi+\left(D-2\right)\left(1-D\right)\left(\nabla\phi\right)^{2}
\end{eqnarray*}](/_static/latex/6a58c5a5b413ae87d0905845f54c1c27.gif "\begin{eqnarray*}
\tilde{R}_{\nu\sigma} & = & R_{\nu\sigma}+(2-D)\left[ \nabla_\nu\nabla_\sigma \phi - \nabla_\nu \phi \nabla_\sigma \phi \right] \\
& & - g_{\nu\sigma} \left[ \nabla^\mu \nabla_\mu \phi + (D-2) \nabla_\mu \phi \nabla^\mu \phi \right] \\
\tilde{R} & = & R+2(1-D)\nabla^{2}\phi+\left(D-2\right)\left(1-D\right)\left(\nabla\phi\right)^{2}
\end{eqnarray*}")
where all covariant derivatives are measured in the unaltered metric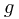 
, and all indices are raised and lowered using this metric too.