Rarita Schwinger (Spin 3/2) Fields
Introduction and Representations
In principle, analysis of the representation theory of the Lorentz group (or rather its double cover) allows arbitrary  representations to exist physically. However, all physical fields corresponding to known particles (using the word 'known' loosely regarding gravitons) are in:
representations to exist physically. However, all physical fields corresponding to known particles (using the word 'known' loosely regarding gravitons) are in:
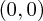 representation - so spin 0 or scalar particles. Specifically the Higgs particle lives here.
representation - so spin 0 or scalar particles. Specifically the Higgs particle lives here. representation or either of its two irreducible parts - so spin 1/2 Dirac (or Majorana, which are Dirac with a reality constraint) or Weyl spinors particles. All the known 'matter' particles live here - the quarks and leptons.
representation or either of its two irreducible parts - so spin 1/2 Dirac (or Majorana, which are Dirac with a reality constraint) or Weyl spinors particles. All the known 'matter' particles live here - the quarks and leptons.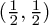 representation - so spin 1 or vector particles. The best known quantum forces are mediated by gauge bosons in these representations - gluons for QCD, the various weak bosons and the photon.
representation - so spin 1 or vector particles. The best known quantum forces are mediated by gauge bosons in these representations - gluons for QCD, the various weak bosons and the photon. representation - so spin 2 or tensor particles. This decomposition makes up a symmetric, two-index tensor
representation - so spin 2 or tensor particles. This decomposition makes up a symmetric, two-index tensor 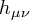 which is the graviton; the scalar part is its trace.
which is the graviton; the scalar part is its trace.
However, in studying supergravity - the supersymmetric completion of gravity - one needs a (massless) spin 3/2 particle to partner up with the graviton. This gravitino is naïvely taken to be a vector-spinor meaning that it has one index of each type, as in 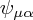 . This has 16 components which are roughly speaking real or complex according to whether the field is 'Dirac' or 'Majorana' in a generalized sense (given simply by imposing the corresponding condition for each value of the spacetime index).
. This has 16 components which are roughly speaking real or complex according to whether the field is 'Dirac' or 'Majorana' in a generalized sense (given simply by imposing the corresponding condition for each value of the spacetime index).
Computing the representation, however, we find that by tensoring together these representations we get more than we wanted. Firstly, note
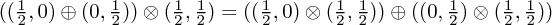
and now recall the  rule that
rule that 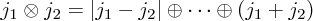 to conclude that we have
to conclude that we have

In particular, we observe that there are components of the vector-spinor which transform as spin 1/2 fields, which is perhaps surprising or undesirable.
However, it turns out that the massless theory is naturally described by a gauge theory. This is slightly surprising at first, finding a fermionic gauge redundancy, but on reflection this is simply because we've only looked at spin 1/2 fermions before, whereas we've come across spin 0, 1 and 2 bosonic fields. Amongst other things, it turns out that this gauge redundancy makes the spin 1/2 parts of the field go away - that is, they correspond to pure gauge.
The Theory
So what exactly is this theory? It is described by a field  as mentioned above, and has a Lagrangian in 3+1 dimensions of
as mentioned above, and has a Lagrangian in 3+1 dimensions of

(Here the gamma matrices in 4D are used. The factor of 1/2 corrects the kinetic term for the smaller number of degrees of freedom - for the Majorana case the barred spinor is not independent of the unbarred one. The above Lagrangians are sensitive in their overall phases to sign conventions, and in overall constants to normalization - we won't worry about this.)
There is an alternative version of this Lagrangian which avoids the obviously (due to the fifth gamma matrix and use of epsilon with four indices) four-dimensional nature of the above, given by
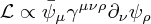
where one denotes the antisymmetrized products of gamma matrices by
![\gamma^{\mu \nu \cdots \rho} = \gamma^{[\mu} \gamma^{\nu} \cdots \gamma^{\rho]} \gamma^{\mu \nu \cdots \rho} = \gamma^{[\mu} \gamma^{\nu} \cdots \gamma^{\rho]}](/_static/latex/37861070f110ce4db49b69fba0613a3c.png)
This is obtained simply by working out an identity involving the gamma matrices.
Equations of motion
The equations of motion in the Dirac case are easy to deduce (and are identical in the Majorana case) - one finds two equivalent equations
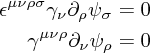
Gauge redundancy and degrees of freedom
The interesting thing about these fields is that they have a gauge redundancy given by
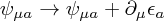
for any Dirac/Majorana (according to the nature of the spin 3/2 field) spinor field  .
.
This precisely conspires to remove the spin 1/2 degrees of freedom spotted above, reducing the number of degrees of freedom (counting in the Majorana case where each component is real for simplicity) down from 16 to 12.
One must also realize that the 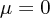 components appear without any time derivatives in the action, and are therefore non-dynamical (determined by the other components). As a result, one can eliminate a further four degrees of freedom, bringing us down to 8.
components appear without any time derivatives in the action, and are therefore non-dynamical (determined by the other components). As a result, one can eliminate a further four degrees of freedom, bringing us down to 8.
But also we find that the corresponding equation of motion is a constraint equation, imposing four further independent constraints, and leaving us with merely 4 degrees of freedom.
Finally, the fact that the Lagrangian is first-order in derivatives also serves its usual purpose of halving the apparent degrees of freedom (in the sense that in the phase space momenta conjugate to a given component are given by another component of the field rather than derivatives thereof) so that we have only 2 degrees of freedom - exactly as required to give the two helicity states of such a massless particle in four dimensions.
In terms of equations (see also Gauge Quantization for Spin 3/2 Fields by Das and Freedman), this goes as follows:
- One should pick a gauge for the gravitino. There are choices analogous to the Lorenz and Coulomb choices in electromagnetism (respectively
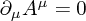 and
and 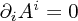 ) given by
) given by
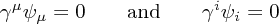 respectively. The former is often called the harmonic gauge. However, we shall use the latter here because it simplifies the analysis of degrees of freedom somewhat. One should note that this gauge choice is always achievable (which is easily checked by writing down an
respectively. The former is often called the harmonic gauge. However, we shall use the latter here because it simplifies the analysis of degrees of freedom somewhat. One should note that this gauge choice is always achievable (which is easily checked by writing down an  for a given
for a given 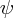 ).
).
- The constraint equation (
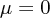 ) gives after a little work
) gives after a little work
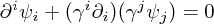 so that by our choice of gauge condition we obtain the constraint
so that by our choice of gauge condition we obtain the constraint 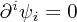
- Also, we may now solve for the
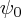 component, because contracting the equation of motion with
component, because contracting the equation of motion with 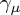 gives one
gives one
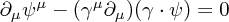 or using our gauge condition and constraint, and cancelling the time derivatives,
or using our gauge condition and constraint, and cancelling the time derivatives,
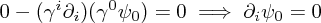 and so
and so 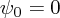 with some further small amount of gauge fixing. (This is possible because if one uses
with some further small amount of gauge fixing. (This is possible because if one uses  depending only on time, one can set this component to zero without affecting the others. Then one requires
depending only on time, one can set this component to zero without affecting the others. Then one requires  to be independent of time.)
to be independent of time.)
A quick remark on gauge fixing: our choice of gauge conditions, as usual, did not quite completely fix the ambiguity in the field, because if we choose 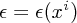 to satisfy
to satisfy 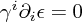 then the resulting gauge-transformed field still obeys the gauge condition(s) but is clearly distinct. However, the space of such functions - namely solutions to the time-independent Dirac equation - is sparse in the space of all gauge transformations, and the degree-of-freedom counting is right.
then the resulting gauge-transformed field still obeys the gauge condition(s) but is clearly distinct. However, the space of such functions - namely solutions to the time-independent Dirac equation - is sparse in the space of all gauge transformations, and the degree-of-freedom counting is right.
The analogy here is with imposing, for instance, the Coulomb gauge condition 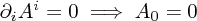 for the electromagnetic field, which leaves one with the ability to transform
for the electromagnetic field, which leaves one with the ability to transform 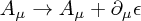 provided the real parameter satisfies
provided the real parameter satisfies 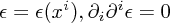 .
.
Resulting theory
Putting this all together, we have the constraints
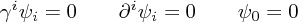
with the remaining gauge redundancy
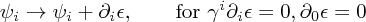
and the equation of motion (using the constraints)
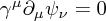
Curved Space Theory
In curved spacetime, with metric and vielbein such that 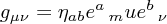 as usual, one needs to define two things to make the theory covariant.
as usual, one needs to define two things to make the theory covariant.
This is all fairly simple, since the spinor indices do not transform under general coordinate transformations. (Spinor fields are sections of the spinor bundle associated to the principal bundle, with indices living in this internal space rather than a spacetime one - local Lorentz transformations on the vielbein or equivalently on the flat space indices can act on the spinors, but not the spacetime transformations.) The upshot is that one can continue writing down a four-component spinor as just a list of four numbers without worrying about picking a basis corresponding to the spacetime coordinates in any sense.
Curved space gamma matrices
Firstly, one has gamma matrices with Lorentz vector indices μ and consequently one needs to make these covariant. Fortunately this is easily done using a vielbein; one defines
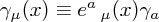
where 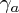 is a constant gamma matrix living in flat space; any of the usual bases like the chiral basis are fine here.
is a constant gamma matrix living in flat space; any of the usual bases like the chiral basis are fine here.
This is part of a general prescription for changing between spacetime indices and vielbein indices; one always simply contracts with the vielbein or its inverse as appropriate. (Recall that the whole vielbein can be thought of as an n × n matrix in n dimensions.)
Spin connection
Slightly more subtle is choosing the correct covariant derivative to act on 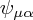 . It's a safe bet that the spacetime index will need us to add on a familiar Christoffel symbol term, but what might the spinor index do?
. It's a safe bet that the spacetime index will need us to add on a familiar Christoffel symbol term, but what might the spinor index do?
It turns out - by considering the effect of a transformation or otherwise - that the correct spin connection for derivatives of a spinor 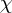 is given by
is given by
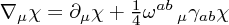
where 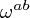 are the curvature one forms for the vielbein, and
are the curvature one forms for the vielbein, and 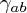 are the antisymmetrized products of gamma matrices mentioned above. (Note that they are the familiar flat space gamma matrices due to the Latin indices.) The curvature one forms, antisymmetric in their two indices, are given as usual by
are the antisymmetrized products of gamma matrices mentioned above. (Note that they are the familiar flat space gamma matrices due to the Latin indices.) The curvature one forms, antisymmetric in their two indices, are given as usual by 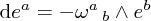 amongst other expressions.
amongst other expressions.
To form a fully covariant derivative acting on the spin 3/2 field, one should simply add the Christoffel symbol term one would if only the vector index was present.
The end result
...
Quantum Theory
In the quantum version of the theory, the 12 redundant degrees of freedom have to be cancelled by ghosts. See also Ghost counting in supergravity (Nielsen).
...