Mathematical Formulation of Quantum Mechanics
Quantum mechanics proposes to explain the behaviour of all physical systems, and its mathematical formulation is, whilst crucial to the successful use of the theory, very abstract.
The following article is designed to provide a gradual introduction of physical concepts and mathematical ideas, by providing a thorough derivation of the basic system. If you have difficulties with the mathematical aspects, please refer to articles on them.
Quantum States & Superposition - Hilbert Spaces
A very large amount of theory can be derived from a relatively small number of ideas in quantum mechanical - the mathematical tools available are very powerful. We shall construct the theory 'from the bottom up', avoiding using complicated mathematical structures without justification; more concise constructions are possible (see the derivation from von Neumann's postulates).
The following section introduces - and explains the rationale behind - the use of a vector space (specifically, a Hilbert space) in quantum mechanics. Let us begin with a simple convention:
Valid states of a physical system are to be denoted by 'kets' like 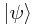 and
and 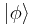 (Greek letters, like these - psi and phi - are generally used). A ket contains a description of the given system - specifically, a description of the values of the degrees of freedom of the system.
(Greek letters, like these - psi and phi - are generally used). A ket contains a description of the given system - specifically, a description of the values of the degrees of freedom of the system.
The Principle of Superposition
We will introduce the mathematical formalism with two important examples in which the phenomenon known as 'superposition' is noticeable: the polarization of photons, and the interference of light.
Polarization
Consider a crystal which only transmits light which is (plane) polarized perpendicularly to the optic axis of the crystal. Now all photons of light (individual particles) coming through from the far side of the crystal are polarized in this way, a fact observable, for instance, by recording the direction of electrons ejected from a metal surface in a photo-electric experiment. Now let us measure the intensity of light (which is equivalent to the fraction of photons received on the far side) varies with the angle of polarization of the light incident on the crystal:
- If the beam is polarized perpendicular to the optic axis (call this state
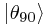 ), it all passes through.
), it all passes through. - If it is polarized parallel to the optic axis (
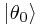 ), none of it passes through.
), none of it passes through. - If it is polarized at an angle
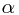 to the optic axis, in the state
to the optic axis, in the state 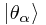 , then
, then 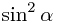 of the light passes through.
of the light passes through.
The first two facts seem straightforward enough from a classical standpoint. However, we struggle to understand the last point, as it is fundamentally probabilistic in nature - that is to say, at an angle of, say, 45° (in the state 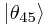 ), 50% of the photons emerge (in the state
), 50% of the photons emerge (in the state 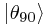 ), and 50% do not, and it is (to the best of our knowledge) impossible to predict what any given photon will actually do.
), and 50% do not, and it is (to the best of our knowledge) impossible to predict what any given photon will actually do.
Using our state notation, it appears that a photon initially in state 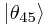 has 'jumped' into a different state,
has 'jumped' into a different state, 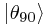 , with probability 50%. This works for any other angle, with the given probability, where
, with probability 50%. This works for any other angle, with the given probability, where 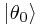 never performs the leap since the probability is 0.
never performs the leap since the probability is 0.
The so-called Principle of Superposition suggests that we imagine the state 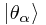 to actually be a weighted mixture of the two possible states
to actually be a weighted mixture of the two possible states 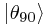 and
and 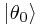 . The following principle expresses this in the general case:
. The following principle expresses this in the general case:
The Principle of Superposition: If we have two valid states of a physical system, denoted by 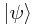 and
and 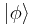 , then any linear combination of them is also a valid state (excluding the null ket
, then any linear combination of them is also a valid state (excluding the null ket 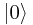 formed by multiplying a valid state by 0), and if we write any state in terms of mutually contradictory states, then the ratio of the coefficients to one another specifies how likely the system is to be in each state when a measurement is made.
formed by multiplying a valid state by 0), and if we write any state in terms of mutually contradictory states, then the ratio of the coefficients to one another specifies how likely the system is to be in each state when a measurement is made.
This means that, for example, we might write 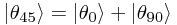 with both coefficients equal to 1 to show that in this case the outcomes are equally likely.
with both coefficients equal to 1 to show that in this case the outcomes are equally likely.
However, consider 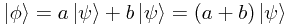 Clearly,
Clearly, 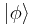 is a combination of
is a combination of 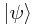 with itself, and hence actually represents the same quantum state as
with itself, and hence actually represents the same quantum state as 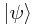 .
.
Therefore, since 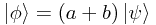 is equivalent to
is equivalent to 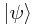 , we can conclude that scale factors do not change the state represented.
, we can conclude that scale factors do not change the state represented.
Interference of Light
A similar experiment with the position and momentum of photons indicates the more general nature of the Principle of Superposition.
Consider a simple double-slit interferometer, which separates a beam of monochromatic light into two beams, and then causes them to interfere, producing a clear interference pattern. As before, by considering what happens in passing individual photons, one at a time, through the apparatus, we can deduce the probabilistic nature of the photon's path.
Our concept of 'state' now involves both a region of space and a momentum - given knowledge of the possible region of space which the photon occupies, we can deduce its momentum, and vice versa.
So consider the state of a single photon entering the interferometer and passing through. We immediately find that its state is, in fact, the superposition of those two states in which the photon passes through one slit, 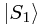 , or the other,
, or the other, 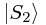 , ignoring for the minute the infinite, continuous range of exact states which could lead a photon through either slit, since when it has emerged and collides with our screen, it is observed to fall in with the general probability distribution which describes the interference pattern expected from waves following both paths.
, ignoring for the minute the infinite, continuous range of exact states which could lead a photon through either slit, since when it has emerged and collides with our screen, it is observed to fall in with the general probability distribution which describes the interference pattern expected from waves following both paths.
A common misconception must be dismissed here: in no way do the photons interfere with each other (this would break energy conservation laws). The probabilities calculated represent the possible position of one photon, rather than the possible number of photons in one position.
The wave functions of the two separate states 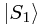 and
and 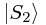 are interacting in the same way that the wave-functions of classical waves interact; but the difference is simply that our new wave functions describe probabilities, whereas the classical wave functions describe a continuous fluctuating actuality.
are interacting in the same way that the wave-functions of classical waves interact; but the difference is simply that our new wave functions describe probabilities, whereas the classical wave functions describe a continuous fluctuating actuality.
So what is a 'wave function'? It is simply another way of saying that the actual state of a system is determined by the probabilities that the system turns out to be in various other particular states when a measurement is made - so the wave function is a way of getting the coefficient in the above expansion by passing the destination state. The 'wave' is a plot of the different 'probability densities'.
Note that any attempt to observe the path of a given photon inside the interferometer will destroy the interference pattern, 'collapsing the wave function' by eliminating possibilities. This applies even if the photon passes through a slit which is not observed, so long as the other slit is. The seemingly paradoxical nature of such a causality is well recognized (the final distribution of the light is affected by the attempt to observe something which does not even necessarily happen) but misleading.
Relative Phase of Components
Let us think carefully about the interference experiment - what we have here is two different non-zero states being added together to produce a zero probability state; that is, if you use a single slit, there is a spread of photons on the wall, but when you open the other one (add the second state) there are some places inside that spread where no photons will appear.
So the coefficients must be allowed to be negative - then, the two wave functions may cancel out at some points (where they are of different sign) and add together (where they have the same sign). These effects produce minima and maxima of intensity respectively.
But since the superposition of the wave functions does suddenly change from large to zero, but rather goes through intermediate intensities, and since the probability densities of the original wave functions do not themselves oscillate, the wave functions' actual value must oscillate cyclically, from positive to negative and back again, without passing through 0. The solution is to introduce a complex phase factor 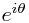 (as realized by Schrödinger in 1925), so that the modulus of the wave function is unaltered.
(as realized by Schrödinger in 1925), so that the modulus of the wave function is unaltered.
This means that whilst the wave function now expresses two pieces of information:
- Density, related to the modulus of the wave function,
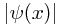 , continues to represent, in some way, the probability (density). (The density is actually the modulus squared of the wave function, as we shall see later.)
, continues to represent, in some way, the probability (density). (The density is actually the modulus squared of the wave function, as we shall see later.) - Phase factor, the argument or angle of the wave function,
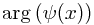 , is not a physical property of the system, but the relative phase factor of two waves controls how they interfere or superpose.
, is not a physical property of the system, but the relative phase factor of two waves controls how they interfere or superpose.
(Introducing a complex phase factor also allows the construction of circularly or elliptically polarized photons; 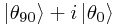 corresponds to a circularly polarized photon.)
corresponds to a circularly polarized photon.)
It is reasonable to assume that the phase (the angle θ) changes linearly with respect to time in a propagating wave, and this is indeed the case, as we shall see later.
For example, let us imagine we have two slits at 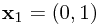 and
and 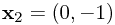 . Without loss of generality, let the wave functions be real and positive at their slits. Also, let us say that the rate of change of phase with respect to distance from the slit varies at the rate
. Without loss of generality, let the wave functions be real and positive at their slits. Also, let us say that the rate of change of phase with respect to distance from the slit varies at the rate 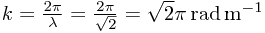 (k is the wave number and λ is the wave length); that is, after
(k is the wave number and λ is the wave length); that is, after 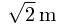 (the wavelength), the wave function is once more real and positive.
(the wavelength), the wave function is once more real and positive.
Then at the point 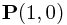 , since P is equidistant from the two slits, the two wave functions are in phase, and add constructively, giving the central maxima familiar from double-slit diffraction experiments. Specifically, the phase has changed by
, since P is equidistant from the two slits, the two wave functions are in phase, and add constructively, giving the central maxima familiar from double-slit diffraction experiments. Specifically, the phase has changed by 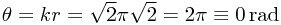 so both wave functions are real and positive, and
so both wave functions are real and positive, and 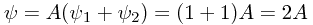 where A is the common coefficient in the superposition. (Note that if P had been at any other equidistant point, the two waves would have been in phase, but not necessarily have been real and positive - but that this does not make a physical difference.)
where A is the common coefficient in the superposition. (Note that if P had been at any other equidistant point, the two waves would have been in phase, but not necessarily have been real and positive - but that this does not make a physical difference.)
By way of contrast, at the point 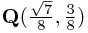 which is
which is 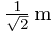 from the first slit and
from the first slit and 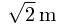 from the second, the two wave functions have values
from the second, the two wave functions have values 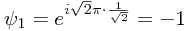 and
and 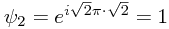 so there is no resultant amplitude, and this is a minimum.
so there is no resultant amplitude, and this is a minimum.
Finally, at the point 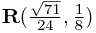 which is
which is 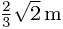 from the first slit and
from the first slit and 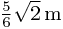 from the second, the two wave functions have values
from the second, the two wave functions have values 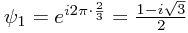 and
and 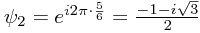 , so the resultant amplitude is
, so the resultant amplitude is 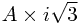 , with a modulus of around 1.73A.
, with a modulus of around 1.73A.
Ket Space
At this point it is worth considering what type of mathematical objects our kets are, and what sort of space they are residing in.
- We have defined an addition operator that is clearly commutative (
 since they represent the same state).
since they represent the same state). - We are interested in some property other than the magnitude of the ket, since scale factors have no effect on the physical interpretation.
- The space must be complex, since kets can store complex numbers.
- Any ket in the space can be decomposed into any complete set of mutually contradictory kets, none of which can be decomposed into a collection of the others.
The major clue in this set-up is the last point - the quality described is exactly that of the linear independence of a basis in a vector space. That is, each mutually contradictory ket corresponds to a dimension (which is entirely abstract) in the vector space, and the magnitude of the component ('coordinate') in that dimension is the probability amplitude (which will have, in addition to size, a phase which has no meaning as an angle in the vector space).
Choosing a different set of mutually contradictory kets is just like choosing another coordinate system - so long as the basis (the mutually contradictory kets) are complete, all the information will be preserved.
It is important to realize that coordinate positions in the ket space does not correspond to any physical position - in fact, a continuous range of possible positions is represented by an infinite set of dimensions, with the complex coordinates representing probability amplitudes. That is to say, there is a dimension for x = 0, 1, ... and x = 0.1, 0.2, 0.3, ... and x = 0.01, 0.02, ... and so on.
In fact, ket space is a complex vector space, and an inner product space - specifically a Hilbert space. (Note that Hilbert spaces have an additional requirement - that the space be 'complete', in the sense that any sequence that converges and is Cauchy has its limit in the space. This seems to makes sense physically - if there is a sequence of states steadily approaching some finite limit, it seems logical to expect that limit to be attainable.)
The second point above indicates that quantum states are represented by rays in the Hilbert space - that is, the length of the whole ket in the space does not represent anything in particular; rather, the direction determines the state. It is useful, therefore, to use normalized kets wherever possible, so that all kets have length 1.
Introducing a inner product space formalism, however, begs the question - what does any inner product represent? To answer this question, we must first consider so-called linear functionals on the ket space.
Bra Space - Linear Functionals
One of the fundamental principles of quantum mechanics is this:
Linearity of state evolution: It is assumed that the outcomes of all measurements and evolution in a quantum system respect the linearity of the ket composition.
This implies that if, for example,
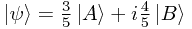 and the system ψ is forced to jump into some state (not simply A or B) then the probability amplitude that it reaches some state φ is given by 0.6 × (the probability amplitude A jumps into φ) plus 0.8i × (the probability amplitude B jumps into φ).
and the system ψ is forced to jump into some state (not simply A or B) then the probability amplitude that it reaches some state φ is given by 0.6 × (the probability amplitude A jumps into φ) plus 0.8i × (the probability amplitude B jumps into φ).
Let us write this symbolically, in terms of some linear functional f:
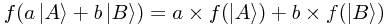
Let us now consider what properties this functional must have, by decomposing some arbitrary ket 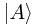 in n-dimensional space (we gloss over nondenumerably infinite spaces here; essentially, sums become integrals) into a basis
in n-dimensional space (we gloss over nondenumerably infinite spaces here; essentially, sums become integrals) into a basis 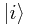 , where i ranges from 1 to n:
, where i ranges from 1 to n:
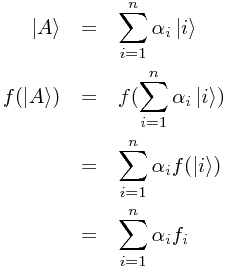 where the
where the 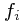 do not depend on
do not depend on 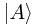 , but instead on the choice of basis.
, but instead on the choice of basis.
This is essentially symmetrical to the definition of the ket! Indeed, if we consider our original motivation - that a functional could extract the complex probability amplitude that the given state transformed into some other specific state - then it is obvious that a ket must have a corresponding functional.
We do, in fact, denote linear functionals on ket space by the complementary notation 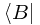 ; this is termed a 'bra', completing the name 'bra-ket' (or bracket), which is another name for this Dirac notation. We can now write
; this is termed a 'bra', completing the name 'bra-ket' (or bracket), which is another name for this Dirac notation. We can now write 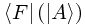 to signify the action of a bra upon a ket, or more concisely,
to signify the action of a bra upon a ket, or more concisely,
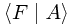
Inner Products
Inner products and bras: A bra is an item, denoted by 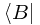 , corresponding to a state B such that the inner product, denoted by
, corresponding to a state B such that the inner product, denoted by 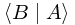 , with any other state A, is the probability amplitude that the state A jumps into the state B when a suitable measurement is made (where a 'suitable measurement' is one in which B is a possible outcome).
, with any other state A, is the probability amplitude that the state A jumps into the state B when a suitable measurement is made (where a 'suitable measurement' is one in which B is a possible outcome).
However, we must look before we leap to a conclusion as to precisely what the relationship between the two sets of coefficients of bras and kets, as there are infinitely many bijections (one-to-one relationships). To see which is the most useful, we will consider the value of the inner product.
From the above, we know that for two states A and B, we can compute the value of
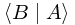 as defined by
as defined by
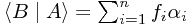 where
where
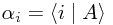 is the (complex) probability amplitude A jumps into the ith basis state.
is the (complex) probability amplitude A jumps into the ith basis state.
Clearly, by the definition, any state must have the property
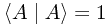 and for any two mutually contradictory states
and for any two mutually contradictory states
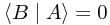
Normalization: A normalized ket is one for which
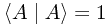 so that we can create a normalized ket from a non-normalized one by the identity
so that we can create a normalized ket from a non-normalized one by the identity
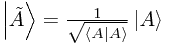
Orthogonality: Pairs or bras and kets, A and B, are orthogonal if and only if
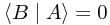
Now consider a ket 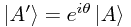 . We've already noted that this must represent the same state as
. We've already noted that this must represent the same state as 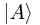 (it's a 'combination' of itself with nothing else), and its length has not changed, since
(it's a 'combination' of itself with nothing else), and its length has not changed, since 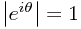 , so we must have
, so we must have
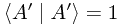 But from this, we can deduce that
But from this, we can deduce that
We can define (up to an irrelevant phase-factor, as always) 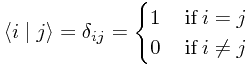
Operators
[...]
Observables and Uncertainty
[...]
Conjugate Variables and Canonical Coordinates
[...]