At the time this was first written, the existence of a boson looking suspiciously like the much sought-after Higgs boson had just been confirmed. This seemed like a good reason to sit down and try and work through the basic intuition behind the ideas which led Higgs & co. to hypothesize the field which manifests itself in the form of this particle. (There will also be an accompanying article on spontaneous symmetry breaking for those of you who want to get a bit deeper into the theory.)

Then, for those interested in the detailed mathematical physics behind it, we'll take a quick look at what sort of thing is actually going on behind the scenes.

The Big Idea

Firstly, there's a lot of waffle which, when boiled down to its core, goes something like this:

"The Higgs boson is what gives matter mass." ~ People

This is loosely draped around fact, but conceals at least three misunderstandings. Since everyone seems to 'know' the above 'fact', let's use these three points to get ourselves a better understanding of what's going on.

Why those people are wrong

1. 'Mass' isn't quite what you think. Firstly, for the above sentence to make any sense, you need to have some idea of what we mean when we talk about mass.

   The two most common notions that make sense to the non-quantum mind are gravitational and inertial mass. The first one tells you about how much of a dent in the rubber sheet of Einstein's universe something makes - how strongly it pulls other things towards it, how strong & far-reaching its gravitational field is. The second one tells you about how fast something goes if you give it some momentum by pushing on it - lighter things go faster for the same amount of momentum.

   But there are two issues with our usual way of thinking about mass, which centers around inertial mass. The first one will make sense classically (without the quantum baggage), and lead us nicely into the point 3, the quantum version of the same thing. The second one is a slightly subtle point about what we mean in the quantum world.

   1. When a ping-pong ball is heavy. One of the simplest and best analogies I know for the way the Higgs mechanism can give mass to things can be explained really easily using one experiment and two things: (i) a ping-pong ball; and (ii) a massive vat of treacle. Like all good experiments.

      The experiment has two stages (followed by a very tasty clean-up). Firstly, pick up the ping-pong ball and move it through the air. You will either be amazed at how light it is, or at your own strength. Either way works fine. Secondly, place the ping-pong ball into the treacle, and move it backwards and forwards. If you want, you can now try this with nearly-set glue or something. You get the idea. End of experiment.

      Hopefully, you noticed that it was a little harder to get the ball moving in the treacle! But why? You can see what is happening a little more clearly with water if you like - the trick is that you're no longer just moving the ball, you have to move the water too! You can even see the ripples.

      I'm being a little quick here - there are actually multiple terms which work against you, but there are two important ones: the familiar one is 'drag', which is the force you feel working against you when you are just trying to move the ball at a constant velocity. The slightly less obvious one is what we're interested in - when you try to change the velocity of the ball, or accelerate it, you find that the liquid tries to carry it along in the same direction it was moving before! This extra inertia (usually just 'mass') is what we're interested in. The liquid gives extra apparent mass to the ball.

      In Newton's equation for the forces on the ball, F = ma, you can include the force this exerts on the ball as some extra mass m*, so that we replace the mass, changing 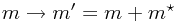. (The 'effective' amount of water you have to move is called the added mass, and in that Wikipedia article they mention that you have to move an effective volume 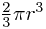of water with a ball of radius r, or half the volume of the ball.) This is why biggish bubbles don't rise ridiculously fast through water compared to an apparently much heavier tennis ball or something!

      For the water analogy, the reason we can get away with bundling the effects of the force into the mass term is simply that the force F_{moving water} is proportional to the acceleration a, so we can factorize 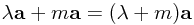. The proportionality ('linearity') aspect is simply a property of the theory for low speeds.

      And that is how the Higgs mechanism works! The ripples show where all the energy you put in goes into the water - the 'field' - instead of the ball/bubble - the 'particle'. The ripples are in some ways like Higgs bosons in the field, as we'll talk about later.

      Aside on bubbles: The point about bubbles mentioned is possibly the best example of how dramatic this added mass can be. The buoyancy force something feels is only a function of how much space it takes up (thanks Archimedes!) so the acceleration something undergoes should be the constant rate of acceleration due to gravity plus something proportional to 1/m by Newton's formula: just divide F_buoyancy - mg = ma by m. Clearly, even a really big bubble (containing just air) is a lot lighter than a tennis ball, but the rate that they accelerate towards the surface isn't that different. Why? Because the bubble gains considerable extra mass, hundreds of times the original mass of the bubble. We'll see below that similar effects with the strong force also have massive implications for the mass of the proton.

   2. What's that little m for?
   When physics gets further from our day-to-day experience, we usually try to give names to things so that they remind us of what they relate to back in that normal world. This is easiest when we have a number in the physics - m, say - and it turns out that "in the classical limit" this appears in exactly the same place in the equations as something we think we understand - mass, say - because then we just go... "Oh great! That must be the mass then!" [We do the same thing in the black hole Schwarzchild solution in general relavity. Only it's a big M because stars are heavier.]

   There was an 'obvious' place that people first put in the m so that it came out to be the mass - it determines how much kinetic energy there is in a wave in the field, just like in the vibration of a drum. This is because (as we discuss below) ripples in a 'field' are observed as the particles of that field. But the problem is that, as we will mention when we discuss the motivation for the Higgs mechanism later, this... turned out to break everything.

   The idea of Higgs & co. was to go a step further back and add a new 'field' which interacted with matter (stuck to it, like the treacle) such that the additional force looked just like there had been an m in there. This worked beautifully, which is why everyone really hoped there was a Higgs field!

   The subtlety I wanted to point out, then, is just that we're talking about a quantum field's property which corresponds to a physical notion of 'mass' in the limit.

   So to summarize: we add on a sticky Higgs field to one original field, and get a much more complicated system - because of something called spontaneous symmetry breaking (to be discussed in another article!) this has a tendency to make the previously massless field get stuck a bit even when there aren't any excitations (particles) in the Higgs field.

   (Without SSB, we would need loads of Higgs particles bouncing around to actually have any effect on other matter, which isn't going to be very evenly affected! For example, there's no effect of electric charge away from... electric charges. Usually, the only possible default [ground] state of a quantum field is the truly empty vacuum 'symmetric' solution, zero. This is symmetric in the sense that you couldn't really choose the field to be anything else without choosing a preferred value; e.g. should the value be +1 or -1? This symmetry has to be broken in a neat way to allow the Higgs field to interact with other fields without loads of particles bouncing around.)

   This means that particles - ripples - in the original field now propagate more slowly, and, in the classical limit, behave like they have a mass, which is just a number (coming from how strongly the Higgs field sticks to the original field).

2. It's not actually where most 'mass' comes from. This point isn't actually too tough to get to grips with, though it might be quite surprising.

   If you look at the list of fundamental particles in the Standard Model^[Wiki], then it is true that the theory says none of these particles would appear to have any 'mass' without the Higgs mechanism. But it is not true that most of the mass of your average elephant is because of interactions with the Higgs field. Why? Because E = mc².

   Sorry, always wanted to say that. The point is that - according to Einstein's highly successful theory of relativity - there isn't really a difference between the presence of energy and the presence of mass. Einstein's famous formula gives a simple relationship between the energy present in a thing and the apparent mass of that thing. This means that if there's any energy inside you - or a proton in an atom say - then this will increase how much mass you seem to have inside! Is this relevant? It turns out that yes, it is very relevant!

   Take a proton, for example. Physicists usually say "it's made up of three quarks - two up, one down". We write the proton p as uud for short. But let's check out the masses of these things. The quark masses here are due to the Higgs mechanism:

   Particle	Approximate bare rest mass (in energy units)...	and in (surprise) mass units
   Up quark u	2.4 MeV/c2	8.6 × 10-30 kg
   Down quark d	4.8 MeV/c2	1.7 × 10-29 kg
   2 × u plus d	9.6 MeV/c2	3.4 × 10-29 kg
   Proton uud	938.3 MeV/c2	1.7 × 10-27 kg

   Whoa. So actually most of the mass of the proton is due to energy - which is why I was careful to say we "usually say it's made of three quarks"! In a very real sense, 99% is not quarks, but energy! One way of looking at this is to say that the extra energy is carried by gluons, the particles of the fields which carry the strong force, in QCD. (Check out the next section for more on fields vs. particles!) Alternatively, people distinguish between current quarks, the quark without colour/strong-force interactions, and constituent quarks, where we also count the gluon field.

   Aside: This is probably more accurate, since the energy is present in the field regardless of what rippling fluctuations - the particles - we say are present. But everything's quantum, so in another sense it's completely pointless to try and make sense of anything like this. (One problem - swept under the carpet in the "approximate bare rest mass" of the heading above - is that due to a very annoying phenomenon called colour confinement it's basically impossible to look at a single quark on its own. If you struggle really hard, and pull one away from the other ones it's currently attached to, you need so much energy a new pair of quarks pop into being and pair up with the one you just pulled away again. Cool, huh?) Indeed, this extra field energy is a vaguely similar, though distinct, sort of phenomenon to the way the interaction with the Higgs field increases the apparent mass of fundamental particles - and as we'll see below, this is best thought of in terms of the field.

   You may be wondering about whether other forces, like electromagnetism, contribute much to mass. It turns out the answer is no; the dominant contribution to the mass of you or me is determined by the energy in the gluon fields! Probably only about 1% of your weight (hundreds of grams) of you is due to the Higgs field energy. But for an electron or a hypothetical bare quark - they're 100% Higgs!

3. It's the field, not the particle. The final thing that's good to realize is what we mean by 'field' and what we mean by 'particle'.

   Given you've made it this far, you've probably heard of wave-particle duality, even if you don't know exactly what it means. Quantum Field Theory is the best way of looking at this phenomenon. In this theory, the fundamental things are not particles, but fields. Just like looking down on a sea, and seeing the surface at different heights in different places, all of spacetime has fields with different strengths (and phases, and possibly directions...). Then waves in the sea can hit each other (though this happens more in baths probably), and bounce off each other and so on. This is the analogy for how particles - which are little ripples in the fields - can bounce off each other. It's complicated by the fact that different types of particle have different fields, but they exist at the same point in our spatial dimensions; but the idea is sound.

   Now remember how we used the image of a wake of ripples in the Higgs field to suggest how it can add mass/energy above? And similarly the mess in the gluon fields inside protons? Well, would you say that it was the ripples that gave the ping-pong ball mass? Perhaps you would, but I would prefer to say that it was the water (and the way it gets pushed around by the ball) that caused the problems.

   In the quantum context, it is slightly more complicated - but it is very definitely the case that the Higgs field is what you need to give mass to fundamental particles. 'The' Higgs boson - a quantized 'ripple' in the field, or an associated particle - is actually more of an accident of the theory. Strictly speaking, the field should have more particles (because it has more degrees of freedom - for mathmos) but these get swallowed up in the interactions with other fields, giving rise to the observed mass.

   The Higgs boson we have sought is the sign of the bit of the theory which got left over - the other sorts of ripples get swallowed up with the fields they are busy giving mass too, and can't run around on their own. But in these theories, you are always left over with an extra Higgs particle, and thankfully we've managed to spot it!

Why do we need/want the Higgs?

Given that we've just shown that most of the mass of the composite things we care about on a day-to-day basis (atoms, for example!) comes from energy in the strong force theories and not from the Higgs field, you might be wondering why it's so important that we have a mechanism for fundamental particles to get mass.

An easy answer to this might be that actually if electrons, for example, didn't have mass, then atomic orbitals wouldn't really work, and we wouldn't get as far as atoms! At least, chemistry would be dramatically different, and at completely different energy scales.

Aside: But what about the other things it gives mass to? One of the most important classes of particles are the gauge bosons, the force-carrying particles of the forces in the Standard Model - these are the photon (in electromagnetism), the W⁺, W^- and Z bosons (of the weak interaction) and the gluons (of the strong force). The Higgs field gives mass to the W⁺, W^- and Z bosons, but not the photon. This is why electromagnetism is a so-called 'long-range' force, with an inverse square law which reaches across space with no particular characteristic length scale, but the weak interaction is short-range, with an exponential decay with distance. The rate at which this decays sets a length scale (the λ in e^r/λ, where r is the distance from the 'source') that is proportional to the inverse mass of the bosons. The decay is because force can be seen as being exchanged by particles 'throwing' force carriers at each other, and they don't get as far if they're heavy!

Aside to the aside: Given that we already mentioned that gluons, the gauge bosons of the strong force, are massless, you might be surprised that the strong force actually appears short-range, acting only on the scale of a proton or neutron. This apparent aberration is due to the colour confinement phenomenon we mentioned before; gluons have colour charge, and so they can't travel far away from their colour-charged companions, constraining the range of the force.

Anyway, let's assume we know we want our fundamental particles to have mass, just to match with experiment. There are two parts to the real answer to the question "Why the Higgs mechanism?"; one is concrete and pretty technical. The other is in parts speculative and elegant. We'll gloss over the technical bits, and focus on the elegance arguments.

1. Technical stuff: renormalization One thing we want our physical theories to do is give answers. In Quantum Field Theory, physicists spend a lot of time getting rid of infinities that appear because the theory wasn't quite written down in the right way. One particularly troublesome infinity comes up when we try to deal with the weak force in 'electroweak' theory, encapsulating both electromagnetism and the weak force.

   The problem is that the best model for the weak force people could come up with had a family of three gauge bosons, the three 'vector' bosons W^± and Z bosons, which can mix together in a very natural way, particularly if we also include electromagnetism (bringing a fourth 'scalar' boson which in the unified theory isn't quite the photon). The sense of 'mixing' is that we can actually cycle around which particle is which without changing the theory - this is a symmetry. (For mathmos, the symmetry groups involved are SU(2) for the mixing of the vector bosons, and U(1) for the scalar boson.) For the theory to work naturally in four-dimensional spacetime, though, we need the 3 vector bosons to arise from a 4D vector.

   3 ≠ 4. This turns out to be a problem unless we can preserve our nice symmetry - with some 'gauge symmetry' we can actually get rid of the fourth degree of freedom by realizing it was an artificial construction, and we can 'renormalize' the theory to give the correct answers without any problems.

   This all goes horribly wrong when the particles have different masses, and as a consequence we don't know how to 'renormalize' the theory to give finite answers. As a result, we want to write down the theory without any masses, so the symmetry we want is still there, and then let something else - the coupling to the Higgs field, for example - generate the right observed masses. This is the strongest original theoretical motivation for the Higgs field.

2. Elegant stuff: from broken symmetries to supersymmetry In the technical discussion just now, we talked a bit about how important symmetries are to us in getting useful theories. They fulfil at least two important functions:
   • Allowing us to make calculations. From pointing out the way to get finite answers from our theories to simply making calculations easier, the symmetries of a theory are very important in letting us actually get numbers out of the theory.
   • Reducing the complexity of the theory. One of the main problems with the Standard Model is that it is full of random disconnected things which come with random numbers - for example, why are there three generations (electron, muon, tau) of leptons which are copies with randomly different masses? Why is the mass of the up quark the number it is (or equivalently, why does it bond to the Higgs field as strongly as it does)? Great progress in physics has often been inunifying apparently unrelated things, like the weak and electromagnetic forces as mentioned above, and historically things like electricity and magnetism!

   So indeed, the way that the Higgs mechanism allows us to dodge the problem of our four electroweak gauge bosons seeming to be related whilst having inconsistent masses is an indication that this is a good way of giving masses to particles!

   But at the moment, the strength of the coupling of the Higgs field to the electroweak fields and the quark fields is still fairly arbitrary. Yet in the great endeavour of modern physics - in which we seek Grand Unificiation Theories (GUTs) that explain everything together, concisely - we can try to simplify the theory by techniques like supersymmetry, in which we predict lots of new particles (which are too heavy for us to make in the laboratory), but fold them together with the existing ones in such a way that the result is actually much more natural!

   Now typically, these theories also need extra Higgs fields, and predict multiple Higgs bosons too, but nonetheless the Higgs mechanism fits in very naturally into the supersymmetric models. If we can identify some supersymmetric-like particles, this would strongly suggest that a model with extra Higgs fields might be a good model of our universe!

   So who knows - perhaps in a few decades we'll be looking for another Higgs boson!

Oh, and as for what it's 'REALLY useful for'...

... have this toast from J J Thomson, the discoverer of the electron:

"To the electron—may it never be of any use to anybody!"

Superconductivity and other analogies

[more to come]

Maths!

[some time... more to come]

You could try The Unapologetic Mathematician's four-part series on the Higgs Mechanism.

The Higgs Mechanism

From the intuition through to the mathematics

Return to top