Euler's Identity
You may have heard of the formula 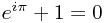 , or
, or  . Intriguing? Or mystifying? Read on...
. Intriguing? Or mystifying? Read on...
Identity Crisis - The "What"
Euler's identity is well renowned because it incorporates 3 mysterious constants integral to pure mathematics, as well as 1 & 0, or -1. These are:
- e: The "base of all natural logarithms" - the integral part, and the first 20 decimal places, of e are 2.71828 18284 59045 23536... See this Wikipedia article for more information.
- π (pi): The ratio of a circle's circumference to its diameter - to 20 decimal places π = 3.14159 26535 89793 23846. See this Wikipedia article for more information.
- i: Also called the "imaginary number", i = √-1. There is no 'decimal expansion' for i, hence its name. Its understanding extended traditional mathematics into "complex mathematics". Again, see the Wikipedia article.
Go Figure - The "Why"
Now, Euler's Identity is a "special case" of Euler's Formula (this means that if a certain set of conditions are satisfied, Euler's Formula turns into Euler's Identity). Consequently, we first need to prove Euler's Formula.
Now, this involves differentiation. If you're not happy with that, I strongly suggest you start with some basic background reading on this subject. WikiBooks makes a great refernce and guide for many subjects. Calculus is no exception, so see the WikiBooks Calculus book's section on differentiation.
When you're happy, particularly with regard to differentiation of the basic trigonometric function, you can begin to analyse Euler's Formula:
Euler's Formula
- Firstly, define the function f(x), where
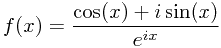 This is 'legal' to differentiate, since it has a value at all points:
This is 'legal' to differentiate, since it has a value at all points: 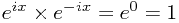 implies that eix at no point equals 0, which would cause a division by zero, making the funcion impossible to differentiate.
implies that eix at no point equals 0, which would cause a division by zero, making the funcion impossible to differentiate. - Now, differentiate this function to obtain f'(x), making use of the quotient rule:
- Put
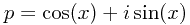 to simplify the writing.
to simplify the writing. - Then
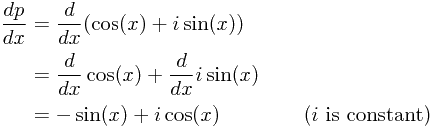
- Therefore:
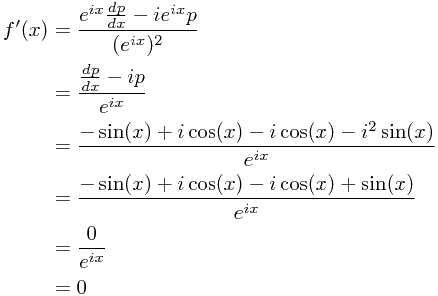
- Put
- If the function differentiates to 0, then it has a rate of change of 0, and so doesn't change. Hence, we can see that
 for any x.
for any x. - So
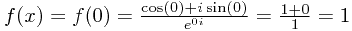 .
. - Now, if
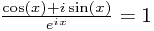 , clearly we have:
, clearly we have:
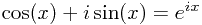 QED
QED
This derivation is known as Euler's Formula, and uses no property of i, except that i × i = -1, and that it is a constant.
Euler's Identity
The conditions for our "special case" are simple: x = π.
Simple evaluating Euler's Formula at this point give us the desired result:
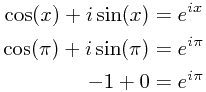
Therefore  and
and 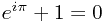 .
.