Vielbeins, metrics and curvature

Written: 09/12/2013 Last edited: 09/12/2013 Filed under: Specialist Topics, Mathematical Physics

Normally, when one has a manifold (or in physics a spacetime), one thinks in terms of the metric which describes how distances work. In a basis, this takes the form of a square, symmetric matrix 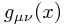$g_{\mu\nu}(x)$ depending on your location on the manifold. It has some other properties, like its signature (the signs -, 0, + of its eigenvalues) which are also constrained. 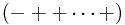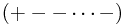The signature is all + for a Riemannian manifold (so that the matrix is positive definite), or either $(-++ \cdots +)$ or $(+-- \cdots -)$ for a Lorentzian manifold, with 'mostly plus' or 'mostly minus' convention respectively.

However, it is often much more convenient to describe the metric in a completely different way. To motivate this, recall the notion of local inertial coordinates in general relativity - this is where one chooses a set of coordinates on the manifold such that the matrix of the metric is flat at some point p. By 'flat', we mean that it is diagonal with only 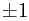$\pm 1$ on the diagonal.

One can only do this at a isolated point p in general for a curved manifold. However, if we allow ourselves a bit more freedom, we can do a bit better.

Choosing coordinates is really just a special way of choosing a basis for the tangent space. This suggests that instead of thinking about choosing coordinates, we should just thinking about choosing bases for the tangent space.

If we want the metric to appear flat in this basis (working in the 4D mostly plus Lorentzian case without real loss of generality), we are seeking a collection of basis vectors 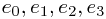$e_0, e_1, e_2, e_3$ at every point of the manifold, such that 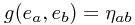$g(e_a, e_b) = \eta_{ab}$ everywhere, where 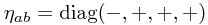$\eta_{ab} = \mathrm{diag}(-,+,+,+)$ . That is, in this basis, $g_{ab} = \eta_{ab}$ .

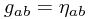If we were in some coordinate basis, this would look like the following:

$g(e_a, e_b) \mid_p = g_{\mu\nu}(x) (e_a(x))^\mu (e_b(x))^\nu = \eta_{ab} \qquad x = x(p)$

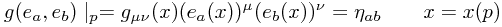
or more concisely

$g(e_a, e_b) = \boxed{g_{\mu\nu} e_a\,^\mu e_b\,^\nu = \eta_{ab}}$

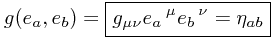
Note that there are now two types of index in our world! The indices 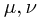$\mu,\nu$ still belong to some particular coordinate basis of the spaceime. However, the indices 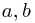$a,b$ belong to a flat world, in the sense that there is only a flat space metric for these indices. Indeed, initially they are simply labels for the four basis vector fields we have chosen.

This collection of vector fields is called a tetrad or vierbein for the metric; the latter is German for four legs. There are generalizations to different dimensions, so for instance in three dimensions one has a triad or dreibein, and so forth. In general, vielbein (many legs) is used to refer to such a collection in arbitrary dimensions.

So what can we say about this set of vector fields? For one thing, they have some redundancy. We are choosing 4 × 4 = 16 components at each point, but we are only satisfying 10 independent equations (due to the automatic symmetry of both sides of the imposed constraint). Where does this redundancy come from? It's not too hard to see that these 6 degrees of freedom for each point in space correspond exactly to the 6 local Lorentz transformations (3 rotations and 3 boosts) acting in the tangent space at each point. That is, one may choose some local Lorentz transformation 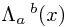$\Lambda_a\,^b(x)$ to the basis vectors to give a new set $e'_a = \Lambda _a\,^b e_b$ .

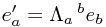Note also that we can rewrite the above relation in various different ways, like

$\eta_{ab} = e_a\,^\mu g_{\mu\nu} e_b\,^\nu = (M g M^\top)_{ab}, \qquad M_a\,^\mu = e_a\,^\mu \text{ a matrix}$

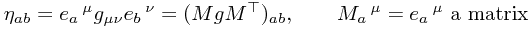
and therefore

$\eta^{-1} = (M^\top)^{-1} g^{-1} M^{-1}, \qquad M^\top \eta^{-1} = g^{-1} M^{-1}$

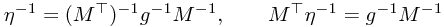
To write these in components, we must define the inverse vielbein. Notice that 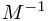$M^{-1}$ must have indices 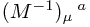$(M^{-1})_\mu\,^a$ . We define the inverse vielbein to be

$e_\mu\,^a \equiv (M^{-1})_\mu\,^a = (g M^\top \eta^{-1})^\mu\,_a = g_{\mu\nu} e_b\,^\nu \eta^{ab}$

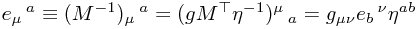
which is in agreement with the result one gest simply by considering raising and lowering indices.

One can also use the above (or a more direct calculation) to observe

$M^\top\eta^{-1} M = g^{-1} \qquad \implies \qquad \boxed{ e_a\,^\mu e_b\,^\nu \eta^{ab} = g^{\mu\nu}}$

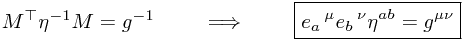
This expresses the fact that the vierbein is very much like the square root of the metric - the metric can be formed by contracting two vierbeins along their flat indices.

In fact, this gives one a way of constructing a vierbein given the metric - this is essentially a Cholesky decomposition of the metric (with diagonal matrix given by 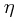$\eta$ ). Another way of doing the construction is simply by Gram-Schmidt orthonormalization.

Curvature

...

Curvature

Vielbeins, metrics and curvature

An introduction to and overview of thinking about metrics in terms of vielbeins

Return to top

suchideas.com

Vielbeins, metrics and curvature

Curvature

Table of Contents

Vielbeins, metrics and curvature

An introduction to and overview of thinking about metrics in terms of vielbeins