Tensor (Direct) Products vs. Direct Sums
A common theme in quantum mechanics and multi-particle systems is manipulation of vector spaces - usually spaces of physical states of a system.
I've come across a little confusion between outer products or tensor products (specifically tensor direct products) and direct sums in this area in particular, so just a quick comparison to make the difference clear:
- Notation: U, V two (for simplicity finite-dimensional) vector spaces with bases u(1), ..., u(l) and v(1), ..., v(m).
| Tensor product | Direct sum | |
|---|---|---|
| What it looks like: | 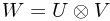 |
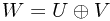 |
| Basis elements: | 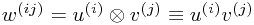 |
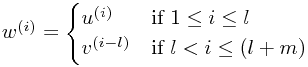 |
| Typical element: | 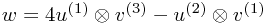 |
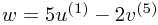 |
| Dimensions: | 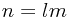 basis elements basis elements |
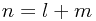 basis elements basis elements |
| Physics: | You need to know information (of different types) from both U and V to describe the system |
U and V represent two alternative (groups of) possibilities for the system, so that you can have a system definitely in a U-type state, for example |
| QM example: | U specifies spin of a particle, V specifies spin of a second (or the position of the first) |
|
More Confusion: Direct Products
Something I fell for when I was writing this down the first time is that there is both a direct product 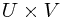 and a tensor (direct) product/outer product
and a tensor (direct) product/outer product 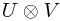 . A direct product is - incredibly confusingly - basically the same as a direct sum in this case.
. A direct product is - incredibly confusingly - basically the same as a direct sum in this case.
A direct product is 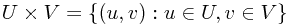 - so each element involves specifying one element of U and one element of V. In the specific case described above - where u and v can be added together - this looks exactly the same as (is isomorphic to) the direct sum. We just write (u,v) ≡ u + v. This is quite general, as you can see in the Wolfram article on direct products.
- so each element involves specifying one element of U and one element of V. In the specific case described above - where u and v can be added together - this looks exactly the same as (is isomorphic to) the direct sum. We just write (u,v) ≡ u + v. This is quite general, as you can see in the Wolfram article on direct products.
If you're wondering what the relationship between a tensor product and a direct product is, it's slightly subtle. The tensor product arises from the free vector space on the direct product 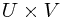 . The idea is that we define one basis vector ('direction') per element of
. The idea is that we define one basis vector ('direction') per element of 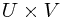 , so there is a basis
, so there is a basis 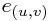 . This is a huge space. (If non-trivial, it is of uncountably infinite dimension here, since each real multiple of one vector corresponds to a new dimension.)
. This is a huge space. (If non-trivial, it is of uncountably infinite dimension here, since each real multiple of one vector corresponds to a new dimension.)
Then we identify basis vectors in a particular way (discussed properly in the Wikipedia article on tensor products) so that addition and scalar multiplication of the elements of 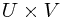 corresponds to addition and multiplication in
corresponds to addition and multiplication in 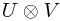 - that is
- that is
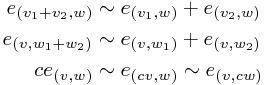
This gets rid of a huge load of basis elements, and leaves us (it turns out!) with the tensor product.
See also: On Wikipedia, the tensor product of Hilbert spaces article provides some more formalism.