Hopf Fibration

Written: 02/12/2014 Last edited: 02/12/2014 Filed under: Specialist Topics, Mathematical Physics

The Hopf fibration is a way to represent 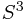S^3 as a fiber of 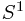S^1 over S^2.

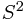The simplest way of writing this fibration down explicitly relies on the identification of 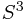S^3 with the set of all rotations of a coordinate basis in three dimensions, which can in turn be visualized as choosing the direction in which (say) the 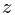z axis points (which is a rotation in 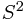S^2) and then rotating in the perpendicular plane to choose the other pair of axes.

Coordinate choice 1

Advantage: gives agreement of the radial coordinate.

Extending this by adding a radial coordinate 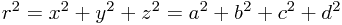r^2=x^2+y^2+z^2=a^2+b^2+c^2+d^2 one finds that the 3D + fiber coordinates 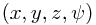(x,y,z,\psi) can be translated to the 4D coordinates 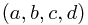(a,b,c,d) via the map

\begin{align*} a &= \sqrt{\frac r {2(r+z)}} (r+z)\cos \psi \\ b &= \sqrt{\frac r {2(r+z)}} \left( x \sin \psi - y \cos \psi \right) \\ c &= \sqrt{\frac r {2(r+z)}} \left( x \cos \psi + y \sin \psi \right) \\ d &= \sqrt{\frac r {2(r+z)}} (r+z) \sin \psi \\ \\ x &= 2(ac+bd)/r \\ y &= 2(-ab+cd)/r \\ z &= (a^2-b^2-c^2+d^2)/r \\ \psi &= \arctan(d/a) \end{align*}

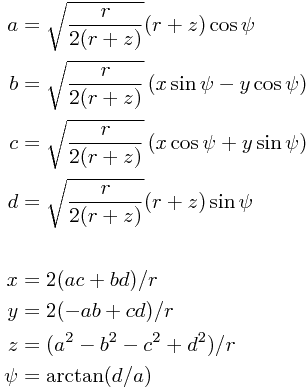
This should be supplemented with the choice 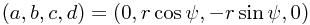(a,b,c,d) = (0,r\cos\psi,-r\sin\psi,0) for (x,y,z,\psi)=(0,0,-r,\psi).

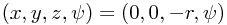Note that in this transformation, one has the radii of the spheres in agreement.

The flat metric on 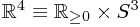\mathbb{R}^4 \equiv \mathbb{R}_{\ge 0} \times S^3 is

\mathrm{d}s^2 = \mathrm{d}a^2 + \mathrm{d}b^2 + \mathrm{d}c^2 + \mathrm{d}d^2

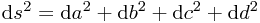
which translates into a metric in the fibred coordinates of

\mathrm{d}s^2 = \mathrm{d}r^2 + \frac 1 4 r^2 (\mathrm{d} \theta^2 + \sin ^2\theta\mathrm{d} \phi^2 + (2\mathrm{d}\psi - (1-\cos\theta)\mathrm{d} \phi)^2)

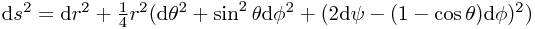
Coordinate choice 2

Advantage: clearer relation to the flat metric in the three-dimensional space. Has nice expressions for 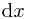\mathrm{d}x etc. in terms of 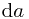\mathrm{d}a etc. (Also one standard form of the near-NUT geometry in Taub-NUT metric.)

Changing the identification of the radial coordinate 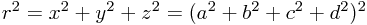r^2=x^2+y^2+z^2=(a^2+b^2+c^2+d^2)^2 one finds that the 3D + fiber coordinates 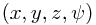(x,y,z,\psi) can be translated to the 4D coordinates 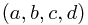(a,b,c,d) via the map

\begin{align*} a &= \sqrt{\frac 1 {2(r+z)}} (r+z)\cos \psi \\ b &= \sqrt{\frac 1 {2(r+z)}} \left( x \sin \psi - y \cos \psi \right) \\ c &= \sqrt{\frac 1 {2(r+z)}} \left( x \cos \psi + y \sin \psi \right) \\ d &= \sqrt{\frac 1 {2(r+z)}} (r+z) \sin \psi \\ \\ x &= 2(ac+bd) \\ y &= 2(-ab+cd) \\ z &= a^2-b^2-c^2+d^2 \\ \psi &= \arctan(d/a) \end{align*}

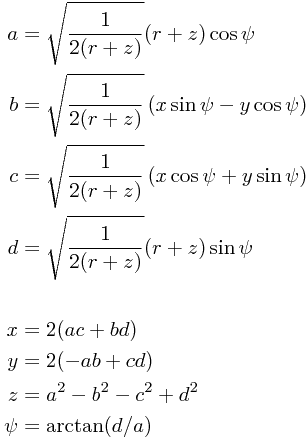
This should be supplemented with the choice 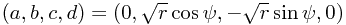(a,b,c,d) = (0,\sqrt{r}\cos\psi,-\sqrt{r}\sin\psi,0) for (x,y,z,\psi)=(0,0,-r,\psi).

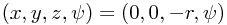We emphasize that the radial directions now scale differently between the two spheres.

The flat metric on 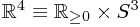\mathbb{R}^4 \equiv \mathbb{R}_{\ge 0} \times S^3 is still

\mathrm{d}s^2 = \mathrm{d}a^2 + \mathrm{d}b^2 + \mathrm{d}c^2 + \mathrm{d}d^2

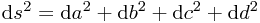
but now this translates into a metric in the fibred coordinates of (noting the factor of 4)

4 \cdot \mathrm{d}s^2 = \frac 1 r \mathrm{d}\mathbf{x}^2 + r(2\mathrm{d}\psi - (1-\cos\theta)\mathrm{d} \phi)^2

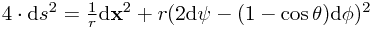
Notice that one has very nice symmetric expressions like 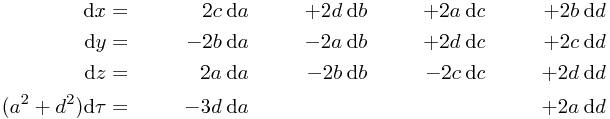\begin{align*} \mathrm{d}x & = &2c & \:\mathrm{d}a &+ 2d & \:\mathrm{d}b &+ 2a & \:\mathrm{d}c &+ 2b & \:\mathrm{d}d \\ \mathrm{d}y & = &-2b & \:\mathrm{d}a &- 2a & \:\mathrm{d}b &+ 2d & \:\mathrm{d}c &+ 2c & \:\mathrm{d}d \\ \mathrm{d}z & = &2a & \:\mathrm{d}a &- 2b & \:\mathrm{d}b &- 2c & \:\mathrm{d}c &+ 2d & \:\mathrm{d}d \\ (a^2+d^2)\mathrm{d}\tau & = &-3d & \:\mathrm{d}a && &&& + 2a & \:\mathrm{d}d \end{align*} in these coordinates.

Hopf Fibration

An explicit coordinate map for the representation of the three-sphere as a circle fibred over the two-sphere

top / xhtml / css
© Carl Turner 2008-2017
design & engine by suchideas / hosted by xenSmart