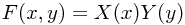Separation of Variables

Written: 12/07/2012 Last edited: 12/07/2012 Filed under: Specialist Topics, Pure Mathematics, Applied Maths

As mentioned to the side, this article will discuss everything from the relevance of Stone-Weierstrass to practical aspects of solving differential equations.

For now though, there's just this cute observation about a condition for a nice smooth function to be multiplicatively separable:

A (twice continuously differentiable) function F(x,y) (away from areas where it or its derivatives are zero) can be decomposed as F(x,y) = X(x) Y(y) if and only if it satisfies the differential equation

$F_x F_y = F F_{xy}$

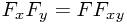
This obviously holds if the function is separable in this way:

$F_x F_y = (X'Y)\cdot(XY') = (XY)\cdot(X'Y') = F F_{xy}$

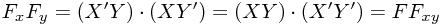
The other way was slightly surprising the first time I noticed it (trying to simplify a GR metric, in fact):

First, rearrange the equation as

$\frac{F_y}{F} = \frac{F_{xy}}{F_x}$

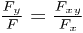
And then observe that this takes the form of the y derivative of logarithms:

$\partial_y \log F = \partial_y \log F_x$

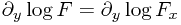
which can easily be integrated to give

$F = F_x \times g(x)$

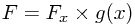
for some function g(x) coming from the 'constant' of integration (which was with respect to y). But now we can rearrange and integrate once more to find

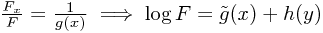$\frac{F_x}{F} = \frac{1}{g(x)} \implies \log F = \tilde{g}(x) + h(y)$ from which we obtain $F(x,y) = X(x) Y(y)$

Separation of Variables

A discussion ranging from the abstract theory of Stone-Weierstrass to the practicalities of solving problems

Return to top