Phase Differences

Written: 29/01/2009 Last edited: 31/07/2009 Filed under: Applied Maths

Consider two waves with equal frequency and amplitude, 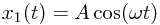$x_1(t)=A\cos(\omega t)$ and $x_2(t)=A\cos(\omega t+\theta)$ .

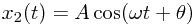The difference between these two waves can be computed as follows:

$\begin{array}{rcl} x_1(t)-x_2(t) & = & A\left[ \cos(\omega t) - \cos(\omega t + \theta) \right] \\ & =& A\left[ \cos(\omega t) - \cos(\omega t)\cos\theta + \sin(\omega t)\sin\theta \right] \\ & =& A\left[ (1-\cos\theta)\times\cos(\omega t) + \sin\theta\times\sin(\omega t) \right] \end{array}$

Now

$\begin{array}{rcl} (1-\cos\theta)^2+\sin^2\theta &= &1+\sin^2\theta+\cos^2\theta-2\cos\theta \\ & =& 2(1-\cos\theta) \end{array}$

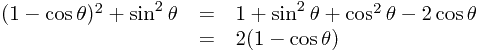
so we may write:

$\begin{array}{rcl} x_1(t)-x_2(t) & = & A\left[ (1-\cos\theta)\times\cos(\omega t) + \sin\theta\times\sin(\omega t) \right] \\ & =& A\sqrt{2(1-\cos\theta)}\Bigl[ \frac{1-\cos\theta}{\sqrt{2(1-\cos\theta)}}\cos(\omega t) + \Bigr. \\ & & \Bigl. + \frac{\sin\theta}{\sqrt{2(1-\cos\theta)}}\sin(\omega t) \Bigr] \\ & =& A\sqrt{2(1-\cos\theta)}\left[ \cos\phi\cos(\omega t) + \sin\phi\sin(\omega t) \right] \\ & =& A\sqrt{2(1-\cos\theta)}\cos(\omega t-\phi) \end{array}$

where we have calculated a new angle 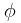$\phi$ using

$\begin{array}{rcl} \cos\phi & =& \frac{1-\cos\theta}{\sqrt{2(1-\cos\theta)}} \\ \sin\phi & =& \frac{\sin\theta}{\sqrt{2(1-\cos\theta)}} \end{array}$

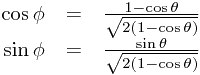
These equations are consistent as a consequence of the division by 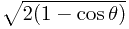$\sqrt{2(1-\cos\theta)}$ .

Hence the maximum value of the difference is 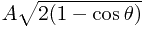$A\sqrt{2(1-\cos\theta)}$ , which is achieved at

$\begin{array}{rcl} \cos(\omega t-\phi) &=& \pm 1 \\ \omega t-\phi &=& 0, \pi, 2\pi, \dots \\ t &=& \frac{1}{\omega} \sin^{-1}\left[ \frac{\sin\theta}{\sqrt{2(1-\cos\theta)}} \right] \dots \end{array}$

Thus given the maximum distance apart of two out-of-phase but otherwise identical oscillators, we simply say:

$\begin{array}{rcl} M &=& A\sqrt{2(1-\cos\theta)} \\ M^2 &=& 2A^2(1-\cos\theta) \\ 1-\cos\theta &=& \frac{M^2}{2A^2} \\ \cos\theta &=& 1-\frac{M^2}{2A^2} \\ \theta &=& \cos^{-1}\left[ 1-\frac{M^2}{2A^2} \right] \end{array}$

Finally, in the case of the maximum being half the amplitude,

$\begin{array}{rcl} \theta &=& \cos^{-1}\left[ 1-\frac{(1/2)^2}{2} \right] \\ &=& \cos^{-1}\left[ 1-\frac{1}{8} \right] \\ &=& \cos^{-1}\left[ \frac{7}{8} \right] \\ &=& 28.96^\circ, 331.04^\circ \end{array}$

Phase Differences

Discrepancies in sinusoidal waves

Return to top