Mathematics
Categories
ContactCourse Notes
Hello! I aim to type up notes for as much mathematics as I can here - in particular, I am drawing on the courses that I attend at Cambridge, gradually supplementing them with useful tricks, interesting extensions and in-depth background to aid the understanding.
Eventually, I hope to integrate these courses into a more encyclopaedic (less course-focused) reference, but for now, this (and good old Wiki P.) will have to do.
Asides - There may be something of interest to you here too!
Please note the usual disclaimers: I take all responsibility for errors in these notes (and surely I will have introduced more than my fair share!), and notes are never a substitute for a good book.
First-Year Courses
Differential Equations
Based on a course delivered by the amazingly clear Professor Grae Worster in 2009:
This course discusses basic techniques in analyzing and solving various classes of differential equation. We begin with a non-rigorous overview of calculus before moving on to analyze increasingly complicated equations, including diversions on to discrete equations, before looking at partial differential equations. (There will soon be a section proving some general results of interest, including the existence and uniqueness of solutions using the contraction mapping theorem.)
Analysis I
Based on a course delivered by the excellent Professor Gabriel Paternain in 2010:
This course discusses the foundations of calculus in a mathematically rigorous manner. We begin by talking about sequences, before moving on to define differentiation in the reals and its underlying ideas. We also introduce power series, before moving on to look at integration. (There will soon be a short section on measure theory, centred on the result that a function is Riemann integrable if and only if the set of its discontinuities has measure zero.)
Second-Year Courses
Variational Principles
Based on a course delivered by Dr. David Stuart in 2010:
This course introduces two core ideas which take optimization first a little, and then a lot, beyond the idea of looking for stationary points of functions. First, the problem of constrained optimization is discussed, where we wish to find the optimum point subject to some given equations. Then, the problem of finding functions which optimize some property - like the length of a curve, for example - is addressed.
Other Courses
Algorithms
Based on a course delivered by Sean Lip in 2010 (course homepage):
This course is a gentle introduction to computer science. It begins by discussing the basic idea of recursion, then moves on to discuss recursion, graph algorithms, greedy algorithms, matchings and network flow. It does all of this from a rigorous, mathematical point of view, discussing the complexity of all algorithms. There are exercises for you to try yourself.
These materials are all currently in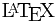 
, authored in the immensely convenient LyX, but I hope to write a converter for my CMS here to transform them into HTML books at some point in the near future.
Please note these are very much works in progress - I want to get around to adding more graphics at some point, as well as integrating them into the website - and several sets of notes are incomplete or missing. For now, use your imagination...
I suggest you either check this page regularly for updates, too, by the way - I try to correct errata as soon as I'm told about them, and I'm constantly adding to them anyway. The contact address is at the top of each PDF, so please don't hesitate to get in touch with anything nice/constructive you'd like to say!
Target Audience?
I hope that these notes are a useful guide for everyone, basically. The mathematics is certainly beyond A-level standard, so if you struggle with the content at that level this perhaps isn't a great place to start. (I do hope to get around to documenting the Mathematics A-levels someday.)
However, if you're an enthusiastic student at that level looking for extension material and background, or a university student looking for a reference with a different point of view, I hope this is the place for you!
Redistribution
These materials are distributed under a permissive Creative Commons licence - you are permitted to use the materials as you wish for non-commercial purposes, but you are required to credit me as the author, and any other people mentioned in each case.
If you have problems with Adobe Acrobat reporting "There was a problem reading this document", then please save the file to your hard drive and open it there. This seems to be a bug with the browser plug-in, particularly with Chrome.