M3: Differential Equations
If you spot any errors, or come up with any improvements, please drop me a line.
Separable First-Order Equations
It's easiest to introduce the idea of these with an example.
A man is pushing a car of mass 1000kg with a force of 200N along a flat track, against a resistive force of strength 2v2N (where v is the speed of the car). If he is trying to get the car to reach a speed of 4ms-1 from rest,
- Find how long the man has to push the car.
- Find out how far the man has to push the car.
Okay, that's quite a lot of information, so we break the problem down into blocks. How many bodies are we interested in the motion of? Only one - the car. This has mass m = 1000. What forces does this body experience? Two forces: 200 forwards, and 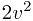 backwards. What do we know about its initial state? Well, at time t = 0, it is at position x = 0, and its velocity is v = 0 (because it is at rest).
backwards. What do we know about its initial state? Well, at time t = 0, it is at position x = 0, and its velocity is v = 0 (because it is at rest).
First, let's write down the simple statement 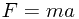 . Now in this equation, we know what F is (because we know all the forces) and we know what m is, but we are not interested in a, since we do not know the acceleration, and we do not want to work it out.
. Now in this equation, we know what F is (because we know all the forces) and we know what m is, but we are not interested in a, since we do not know the acceleration, and we do not want to work it out.
But wait - for part 1, we are interested in t plus we know v, and we know 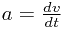 - acceleration is the rate of change of velocity. So we can write
- acceleration is the rate of change of velocity. So we can write 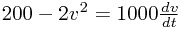 by filling in the sum of forces (remembering the negative backwards force), the mass, and our differential representation of acceleration.
by filling in the sum of forces (remembering the negative backwards force), the mass, and our differential representation of acceleration.
This gives us a formula which relates only time and velocity, which is perfect for answering part 1. Often, we might be asked to rearrange it, usually just by dividing/multiplying by some whole number, to get something like 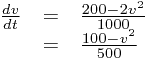 . We've just answered part of the question - forming the differential equation that v satisfies. The problem is, we can't do anything with it next, as it stands.
. We've just answered part of the question - forming the differential equation that v satisfies. The problem is, we can't do anything with it next, as it stands.
The only way we know how to get rid of differentiation is integration, but it's not at all clear what we can integrate at the moment - this is because the variables are mixed up. But - good news! - M3 only contains separable equations; this means that you can always pull apart the two variables:
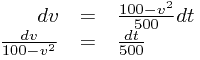
This problem can now be solved by integrating both sides, using the technique of partial fractions to do the v side - we'll do this first:
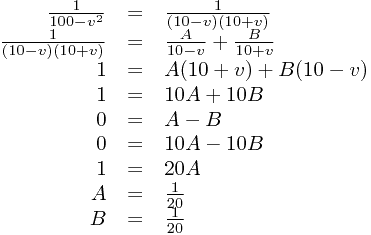
Now we can integrate the function:
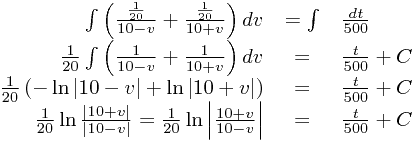 ... which leaves us with a direct relationship between v and t, except for our constant of integration C. There are two ways of dealing with this (that are essentially the same thing); either we integrate using the definite limits of the problem, or we just fill in our initial conditions and solve for C and then work out the answer. We'll demonstrate both methods here - choose the one you prefer!
... which leaves us with a direct relationship between v and t, except for our constant of integration C. There are two ways of dealing with this (that are essentially the same thing); either we integrate using the definite limits of the problem, or we just fill in our initial conditions and solve for C and then work out the answer. We'll demonstrate both methods here - choose the one you prefer!
First, here's the substitution method, using v = 0 when t = 0:
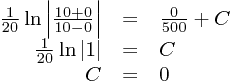 So we can plug in v = 4 and work out t:
So we can plug in v = 4 and work out t:
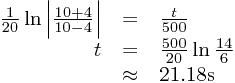
Alternatively, we can use our initial conditions in the limits of our integration. We do the same integration before, except with v being integrated from 0 to 4 (the initial velocity to the final velocity), and with t being integrated from 0 to t (the initial time, to the final time - which is, of course, the unknown we are solving for!):
![\begin{array}{rcl}
\left[\frac{1}{20}\ln\left|\frac{10+v}{10-v}\right|\right]_{0}^{4}&=&\left[\frac{t}{500}\right]_{0}^{t}\\\frac{1}{20}\left(\ln\left|\frac{10+4}{10-4}\right|-\ln\left|\frac{10+0}{10-0}\right|\right)&=&\frac{t-0}{500}\\\frac{1}{20}\left(\ln\frac{14}{6}-\ln1\right)&=&\frac{t}{500}\\t&=&\frac{500}{20}\left(\ln\frac{14}{6}-\ln1\right)\\&\approx&21.18\text{s}
\end{array}
\begin{array}{rcl}
\left[\frac{1}{20}\ln\left|\frac{10+v}{10-v}\right|\right]_{0}^{4}&=&\left[\frac{t}{500}\right]_{0}^{t}\\\frac{1}{20}\left(\ln\left|\frac{10+4}{10-4}\right|-\ln\left|\frac{10+0}{10-0}\right|\right)&=&\frac{t-0}{500}\\\frac{1}{20}\left(\ln\frac{14}{6}-\ln1\right)&=&\frac{t}{500}\\t&=&\frac{500}{20}\left(\ln\frac{14}{6}-\ln1\right)\\&\approx&21.18\text{s}
\end{array}](/_static/latex/bb15465444f9a801401867b2c57efa51.gif)
The second method is probably shorter, since it fits in well with the rest of the question, but the first is possibly easier to understand.
The velocity-displacement form of acceleration
For part 2 of the above question, we are asked to relate velocity (the same 4ms-1) and displacement (which we must calculate). The naïve approach to this might be to try and integrate the velocity-time equation we discovered, and plug in the value of the time we found. However, this is often considerably more difficult (to the point of impossibility) than the following method.
Since, as before, we know F and m in Newton's formula, we might be able to use a different form of a relating velocity and displacement to our advantage here. Consider the 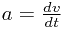 formula we have used above - we want to eliminate time t, but not velocity v, and introduce displacement x. What relates these terms? It is, of course,
formula we have used above - we want to eliminate time t, but not velocity v, and introduce displacement x. What relates these terms? It is, of course, 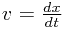 . How can we use this? Well (to use a technically slightly dubious bit of rearranging) this second formula means
. How can we use this? Well (to use a technically slightly dubious bit of rearranging) this second formula means  - substituting this into the first expression gives
- substituting this into the first expression gives 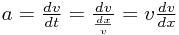 which is exactly the kind of expression we wanted!
which is exactly the kind of expression we wanted!
You should memorize the formula 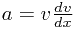 since it makes these questions much easier. Note that we can see it is right (avoiding the dubious line above) by using the Chain Rule:
since it makes these questions much easier. Note that we can see it is right (avoiding the dubious line above) by using the Chain Rule:
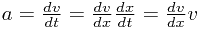
Now we can actually work out the answer to part 2, beginning in exactly the same way as above:
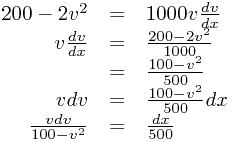
Now this can be integrated more easily than last time, because of the extra v term - the derivative of the denominator is -2v which is very nearly the numerator, so if we divide and multiply by -2 then the function is of the form 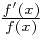 which integrates to
which integrates to 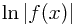 :
:
![\begin{array}{rcl}
\frac{1}{-2}\int_{0}^{4}\frac{-2vdv}{100-v^{2}}&=&\int_{0}^{x}\frac{dx}{500}\\-\frac{1}{2}\left[\ln\left|100-v^{2}\right|\right]_{0}^{4}&=&\frac{x-0}{500}\\x&=&-\frac{1}{2}500\left(\ln\left|100-4^{2}\right|-\ln\left|100-0^{2}\right|\right)\\&=&-250\left(\ln84-\ln100\right)\\&=&250\ln\frac{100}{84}\\&\approx&43.59\text{m}
\end{array}
\begin{array}{rcl}
\frac{1}{-2}\int_{0}^{4}\frac{-2vdv}{100-v^{2}}&=&\int_{0}^{x}\frac{dx}{500}\\-\frac{1}{2}\left[\ln\left|100-v^{2}\right|\right]_{0}^{4}&=&\frac{x-0}{500}\\x&=&-\frac{1}{2}500\left(\ln\left|100-4^{2}\right|-\ln\left|100-0^{2}\right|\right)\\&=&-250\left(\ln84-\ln100\right)\\&=&250\ln\frac{100}{84}\\&\approx&43.59\text{m}
\end{array}](/_static/latex/879256e8e6d436cb946439a31ecd37b3.gif)
Using the Power Equation
When a body is being driven by an engine operating at a constant power, it does not necessarily experience a constant force. This is because the force is smaller at larger velocities: 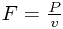 (If you're curious, this comes from differentiating the formula W=F.s, work done is force times distance, with respect to time, giving P=F.v).
(If you're curious, this comes from differentiating the formula W=F.s, work done is force times distance, with respect to time, giving P=F.v).
This makes it possible to work with cars, including those on slopes, like the following:
A car of mass 800kg is driving straight up a hill at 30° to the horizontal against frictional forces of kv2.
- Given it is driving with an engine power of 50kW at a constant speed of 10ms-1, calculate k.
- If the car now turns off its engine,
- how far up the slope would it roll?
- at what speed is it travelling after 5 metres?
- If the car has turned off its engine, and after 5m the road becomes instantaneously flat, at what power would the engine have to work to return to 10ms-1 over the same distance of 5m?
For the first part, we use the fact that the resultant force up and down the slope (the sum of the forces) is 0, since the velocity is not changing.
The driving force is 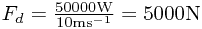 . The two other forces acting are a component of gravity and the resistive force:
. The two other forces acting are a component of gravity and the resistive force: 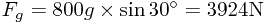 and
and 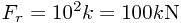 . Therefore
. Therefore
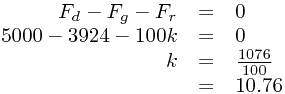
For the next part, we need to form F=ma using the new value of the driving force, 0 - this means also using our velocity-displacement representation of the acceleration:
![\begin{array}{rcl}
0-3924-10.76v^{2}&=&800v\frac{dv}{dx}\\\int_{10}^{v}\frac{-800vdv}{3924+10.76v^{2}}&=&\int_{0}^{x}dx\\x&=&-\frac{800}{2\times10.76}\int_{10}^{v}\frac{2\times10.76vdv}{3924+10.76v^{2}}\\&=&-\frac{10000}{269}\left[\ln\left|3924+10.76v^{2}\right|\right]_{10}^{v}
\end{array}
\begin{array}{rcl}
0-3924-10.76v^{2}&=&800v\frac{dv}{dx}\\\int_{10}^{v}\frac{-800vdv}{3924+10.76v^{2}}&=&\int_{0}^{x}dx\\x&=&-\frac{800}{2\times10.76}\int_{10}^{v}\frac{2\times10.76vdv}{3924+10.76v^{2}}\\&=&-\frac{10000}{269}\left[\ln\left|3924+10.76v^{2}\right|\right]_{10}^{v}
\end{array}](/_static/latex/e6bfae65501ef7582ae8e752835cabe2.gif) which we can expand to
which we can expand to
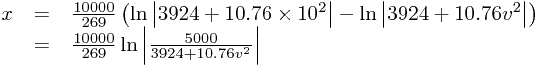
Now firstly, we want the highest point - clearly, this is where v = 0, so
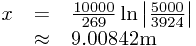
Next, we want to know the velocity v when x = 5:
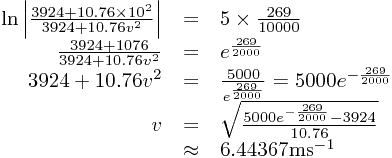
Finally, we consider what happens if the car is suddenly on the level (so Fg = 0) and travelling at this velocity, approximately 6.44367ms-1. We want to calculate the power necessary to reach 10ms-1 in 5m. We form the new force sum, separate the variables, integrate over the appropriate changes in velocity and displacement, and solve the resulting equation for P:
![\begin{array}{rcl}
\sum F=\frac{P}{v}-10.76v^{2}&=&800v\frac{dv}{dx}\\\int_{0}^{5}dx&=&\int_{6.44367}^{10}\frac{800vdv}{\frac{P}{v}-10.76v^{2}}\\5&=&\int_{6.44367}^{10}\frac{800v^{2}dx}{P-10.76v^{3}}\\&=&\frac{800}{-3\times10.76}\int_{6.44367}^{10}\frac{-3\times10.76v^{2}dx}{P-10.76v^{3}}\\&=&\frac{20000}{807}\left[\ln\left|P-10.76v^{3}\right|\right]_{6.44367}^{10}
\end{array}
\begin{array}{rcl}
\sum F=\frac{P}{v}-10.76v^{2}&=&800v\frac{dv}{dx}\\\int_{0}^{5}dx&=&\int_{6.44367}^{10}\frac{800vdv}{\frac{P}{v}-10.76v^{2}}\\5&=&\int_{6.44367}^{10}\frac{800v^{2}dx}{P-10.76v^{3}}\\&=&\frac{800}{-3\times10.76}\int_{6.44367}^{10}\frac{-3\times10.76v^{2}dx}{P-10.76v^{3}}\\&=&\frac{20000}{807}\left[\ln\left|P-10.76v^{3}\right|\right]_{6.44367}^{10}
\end{array}](/_static/latex/8557c93f5a03f4d5cf89ec9d77e7f85f.gif) So
So
![\begin{array}{rcl}
\left[\ln\left|P-10.76v^{3}\right|\right]_{6.44367}^{10}&=&-\frac{807}{4000}\\\ln\left|\frac{P-10.76\times10^{3}}{P-10.76\times6.44367^{3}}\right|&=&-\frac{807}{4000}\\\frac{P-10.76\times10^{3}}{P-10.76\times6.44367^{3}}&=&e^{-\frac{807}{4000}}
\end{array}
\begin{array}{rcl}
\left[\ln\left|P-10.76v^{3}\right|\right]_{6.44367}^{10}&=&-\frac{807}{4000}\\\ln\left|\frac{P-10.76\times10^{3}}{P-10.76\times6.44367^{3}}\right|&=&-\frac{807}{4000}\\\frac{P-10.76\times10^{3}}{P-10.76\times6.44367^{3}}&=&e^{-\frac{807}{4000}}
\end{array}](/_static/latex/833bb67d2b0b34eee4afc9b887383ef8.gif) Now we can solve this for P by multiplying through:
Now we can solve this for P by multiplying through:
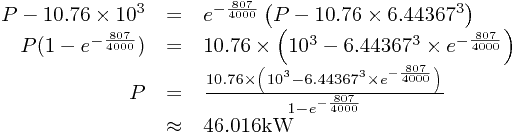
Second-Order Equations
The next problem we come across in our newly discovered differential approach to dynamics is what happens when, for example, the force applied to a particle varies not just with velocity, but displacement or time as well. We can still use similar methods to form differential equations, but we will need entirely new techniques to solve them. First, though, we'll split these equations up into two different types, the first being a special (easier) version of the second:
Homogeneous Equations
As above, let's introduce this topic with an example question:
...