C1: Algebra & Equations
The following guide could probably always be improved... if it can, shout.
Laws of Indices
You are probably familiar with the notation 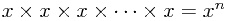 where there are
where there are 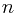 occurences of the
occurences of the 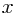 terms, and also with the notation
terms, and also with the notation 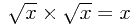 and
and 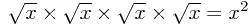 etc,, as well as
etc,, as well as ![\sqrt[3]{x}\sqrt[3]{x}\sqrt[3]{x}=x \sqrt[3]{x}\sqrt[3]{x}\sqrt[3]{x}=x](/_static/latex/6eb6ec94eda0557e74115ed7e8859c4e.gif) .
.
However, we can readily combine these two differenct notations to simplify some of our calculations.
The principle is readily seen from expressions like ![\sqrt[3]{x}\sqrt[3]{x}\sqrt[3]{x}\sqrt[3]{x}\sqrt[3]{x}\sqrt[3]{x}=x^2 \sqrt[3]{x}\sqrt[3]{x}\sqrt[3]{x}\sqrt[3]{x}\sqrt[3]{x}\sqrt[3]{x}=x^2](/_static/latex/2a66737310c6514999cd9624cd159ec4.gif) . We have six occurences of third roots multiplying to give a power of 2. Our logic is then to write
. We have six occurences of third roots multiplying to give a power of 2. Our logic is then to write ![\sqrt[3]{x}=x^{1/3} \sqrt[3]{x}=x^{1/3}](/_static/latex/40dc526da23fdb6b0716f15604b07f06.gif) so that
so that 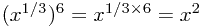 .
.
Also, we use the rule 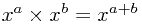 to see that
to see that 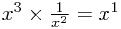 should be written
should be written 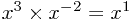 .
.
The laws of indices are then as follows, where the exponents (powers) can be any rational numbers (fractions) which are positive or negative.
![x^{a/b}=\sqrt[b]{x^a}=(\sqrt[b]{x})^a x^{a/b}=\sqrt[b]{x^a}=(\sqrt[b]{x})^a](/_static/latex/038cb854e7f485e092152251070ec149.gif)
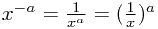

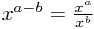
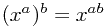
Surds
Sometimes, we come across numbers which incorporate square roots of whole numbers which are not perfect squares, such as 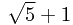 . Since the decimal expansions of these numbers neither stop nor repeat (since they are not rational - fractions of whole numbers), we often find it useful to be able to manipulate these numbers in this same, concise form.
. Since the decimal expansions of these numbers neither stop nor repeat (since they are not rational - fractions of whole numbers), we often find it useful to be able to manipulate these numbers in this same, concise form.
We begin with the basic rules 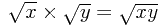 and
and 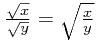
Now we can easily figure out how to add, subtract and multiply surds:
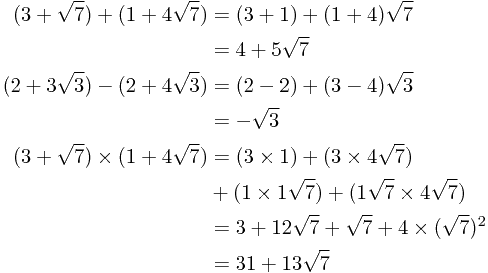
However, this leaves us with the problem of simplifying expressions such as
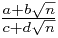
The trick needed is called:
Rationalizing the Denominator
The problem in the division is that the square root on the bottom cannot be easily be divided into the numerator on top.
To resolve this, we would like to transform the denominator into a single number. We do this by multiplying the top and bottom by 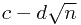 , because the denominator becomes
, because the denominator becomes 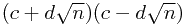 which expands to
which expands to 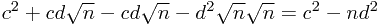 which involves no square roots.
which involves no square roots.
For example:
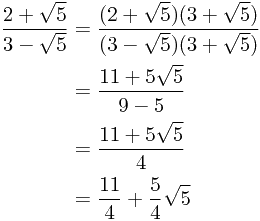 which is much easier to work with in any following manipulations.
which is much easier to work with in any following manipulations.
Quadratics
A quadratic expression is one like this: 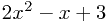 which has no powers of
which has no powers of 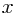 higher than 2.
higher than 2.
Now the easiest way of understanding how an expression like this relates to the value of 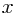 is almost always to plot a graph. So have a look around online for some graphs.
is almost always to plot a graph. So have a look around online for some graphs.
Graphs
What you find is that the graphs all either point up or down in a curve which is symmetrical about the point it stops at (in fact, this particular graph is called a parabola). The ones that point up are those with a negative coefficient of (number multiplying with) 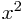 , and those that point down have a positive coefficient.
, and those that point down have a positive coefficient.
Also, because at 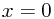 the rest of the formula is zero, the last term (without any x) gives the 'height' at which the curve crosses the (vertical) y axis.
the rest of the formula is zero, the last term (without any x) gives the 'height' at which the curve crosses the (vertical) y axis.
Now, since the graph has one turning point (at its minimum or maximum, depending), it can either:
- stay completely on one side of the (horizontal) x axis and not touch it
- just touch the x-axis at one point
- cross the x-axis at two points
Now, finding where - if anywhere - the curve intersects (crosses) the x-axis is called finding the solution of the equation 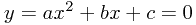
Factorization by Inspection
One of the first methods taught for solving quadratics is by inspection. This means, basically, guesswork or trial-and-error.
This is easiest to explain using an example. Take 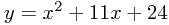 What we want to do is write this as
What we want to do is write this as 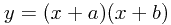 for some new numbers. Let's have a go first.
for some new numbers. Let's have a go first.
If we expand the brackets in what we want, we get
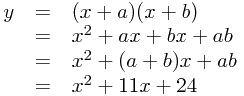 Now by 'comaprison of coefficients' (looking at the bits we multiply by different powers of
Now by 'comaprison of coefficients' (looking at the bits we multiply by different powers of 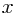 ) we get
) we get
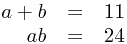 So we want two numbers that add to give 11 and multiply to give 24. Since these are nice whole numbers, we could try listing all the factors of 24 and seeing if they add to give 11. It turns out that
So we want two numbers that add to give 11 and multiply to give 24. Since these are nice whole numbers, we could try listing all the factors of 24 and seeing if they add to give 11. It turns out that 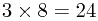 and
and 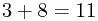 , so
, so
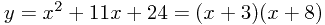
What use is this? Well, what we have here is two numbers, 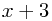 and
and 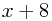 , multiplying together to give
, multiplying together to give 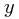 . But if
. But if 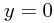 , then at least one of
, then at least one of 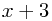 and
and 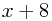 must be zero. This means that either
must be zero. This means that either
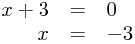 or
or
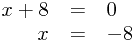 so we have our solutions!
so we have our solutions!
Completing the Square
However, this doesn't always work. Imagine getting decimals or fractions, or something like 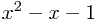 where you can't find whole numbers that multiply and add right. Our next strategy is to complete the square.
where you can't find whole numbers that multiply and add right. Our next strategy is to complete the square.
What this means is writing the original expression 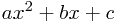 in a different form again. This time, we use
in a different form again. This time, we use 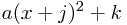 for two new numbers. Let's do what we did for inspection, and expand this:
for two new numbers. Let's do what we did for inspection, and expand this:
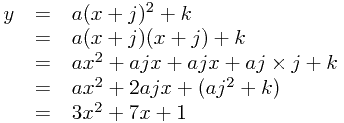 where we've picked a new example. Now, using our old 'comparison of coefficients',
where we've picked a new example. Now, using our old 'comparison of coefficients',
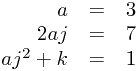
Well, the first line tells us 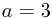 . So in the second line,
. So in the second line, 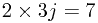 and
and  . Then in the third line,
. Then in the third line, 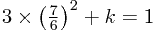 so
so 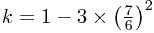 or
or  .
.
Lovely - we now know that
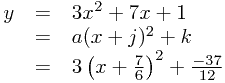 The clever bit here is separating
The clever bit here is separating  from the rest of the equation. This allows us to do several tricks.
from the rest of the equation. This allows us to do several tricks.
The Quadratic Formula
We can also work  out backwards from
out backwards from  when we've completed the square - so if we set
when we've completed the square - so if we set 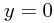 ...
...
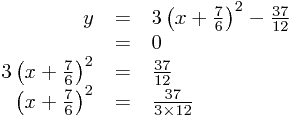 Now we can take square roots (which can be positive or negative!) to get
Now we can take square roots (which can be positive or negative!) to get
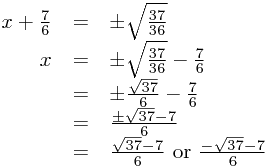
... and those are the solutions!
Now, we can actually use this to derive the next really clever formula from scratch (don't worry - you don't ever have to do this yourself!). Let's say we have 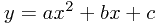 Now to complete the square, we know from above that we end up with
Now to complete the square, we know from above that we end up with
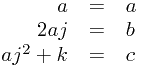 Can you can see why we chose
Can you can see why we chose 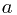 as the number outside the brackets now? Anyway, solving these to work out
as the number outside the brackets now? Anyway, solving these to work out 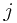 and
and 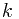 we get
we get
 and
and
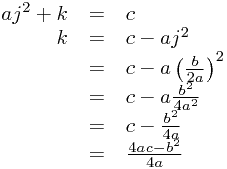
So we know
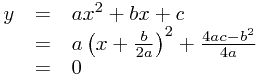 from which we can work out that
from which we can work out that
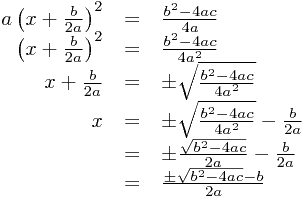 or
or
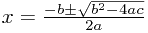 which is known as the quadratic formula, and allows you to work out the solutions of any quadratic equation.
which is known as the quadratic formula, and allows you to work out the solutions of any quadratic equation.