If you've heard of the term spontaneous symmetry breaking, it's quite likely it was in the context of the Higgs mechanism - however, there are other examples in particle physics/quantum field theory (such as the chiral symmetry breaking^[Wiki]) of this phenomenon. It's also a term outside of this narrow area, so we'll start with some other examples - some familiar, one probably less so - just to get us thinking, before moving on to talk more about the particular case of a quantum field with a broken symmetry, like the Higgs field.

The Big Idea

The usual set-up for a spontaneously broken symmetry is that you have some (small or point-like) thing of interest, which can move around in a nice symmetric background landscape, with no particular preferred direction. We start out with some examples:

Two examples

1 - A ball balanced precariously on top of a big round dome on the floor.

A very simple concrete example would be exactly what the heading suggests - you have a situation which has the characteristic lack of a 'preferred' direction, but which nonetheless suddenly develops one as the ball inevitably rolls off the hill to one side.

Of course, in this situation we expect that really there was some slight imperfection in our original situation, which is what gives rise to the eventual obvious broken symmetry. But in the quantum world, even a perfect symmetry can be broken, because the quantum vacuum world has inherent randomness - when observed, it will (eventually) randomly collapse into a nearby lower energy state.

The ball loses potential energy when it rolls down the hill. We call the graph of how much energy it has at different places a potential energy landscape.

2 - A pen balanced precariously on its point

Again, the heading tells you most of what you need to know. Why do I mention this? Because last time you could clearly see the 'hill' which the ball was inclined to roll down - the potential energy landscape was obvious. This time, it's perhaps slightly less clear what is going on.

Since the pen this time falls over to one side, with its point staying still (to begin with), instead of just moving, we might think it was more natural to think about a graph where we plot the energy when the pen is at different angles instead. Then we find that the energy is lower when the pen is at greater angles to the vertical, but the direction in which it tilts away from the vertical doesn't actually affect the energy. Yet when it falls, it falls in a definite direction as before. Here, again, is the broken symmetry.

(If you consider the location centre of mass of the pen, then you can actually make a graph very similar to the one from the first example, but that defeats the point of the example!)

3 - Magnetic alignment

Another slightly more subtle example, much closer to the quantum field case we want to talk about, and probably much less familiar, involves spontaneous magnetization of magnets at low temperatures.

You have certainly come across electromagnets, where a ferromagnetic material - iron, for example - is often put inside coils of wire through which a current is passed. This is done because whilst the coiled wire makes a magnetic field, if we could have a large iron core which was magnetized too, then the magnetic field would be much greater. Indeed, the quantum spins of the particles inside the iron are inclined to line up with the field from the wire they find themselves sitting in, because it is lower energy to do so!

You can imagine this as being like grass which sticks up in random directions until a breeze blows, and bends them all over in the same direction. The trick is that the aligned spins now also have their own little 'winds', or magnetic fields, greatly improving the strength of the magnet.

This is all well and good, but now turn off the wire - and suddenly the random fluctuations due to the thermal energy knocking around inside the iron kick all the spins out of line once more. There is too much energy in the system for it to stay down in the lowest energy state - imagine you kick the ball from the first example - it can roll up and down the hill again!

So, being curious beings, we turn down the thermostat and see what happens. As the material runs out of spare energy for fluctuations, we start to see growing clumps of aligned spins, since they still 'prefer' to line up in each other's fields (that is, it takes energy to continue pointing away from its neighbours). Then, fairly abruptly, the entire material has a single preferred spin direction, and has become completely magnetic with a definite north and south pole! This process has broken the apparent symmetry of the higher-energy system.

Aside: Strictly speaking, the situation is more subtle for metals like iron at room temperature, where local regions of spins are actually aligned in this way, but where there are many such domains with different, randomly distributed preferred directions. All of this is very much statistical physics, and to do with phase transitions!

The quantum field case

So what does all this have to do with a quantum field? The core ideas carry over well, particularly from the magnetic case above. It's worth re-reading that example first if you don't feel quite comfortable with it.

Almost all the time in quantum field theory, one derives the consequences of a theory from the starting point of the Lagrangian, which basically just has information about what the energy of a state of the system is. This is why we talked a lot about energy above.

kinetic energy and potential energy in classical physics - a ball has kinetic energy if it moves, and potential energy from being in a gravitational field. In quantum field theory Lagrangians, we usually divide the types of energy up into kinetic, self-interaction/potential terms (including mass terms), and interaction terms.

• The kinetic terms describe energy due to variation in the field in spacetime, and alone reproduce the equations for a 'free', massless quantum field, with the analogy being with a super-thin rubber sheet - the 1 dimensional version would be a string tied taut between two points. (Confusingly, this means that the 'kinetic' terms in quantum field theory include what would classically be thought of as the potential energy due to the sheet being at different heights in space.)
• A self-interaction term is usually thought of as an energy inherent in having a non-zero value of the field. To put it another way, it needs some energy if you want to disturb the sheet from its natural position, which is usually of lying flat. In particular, the simplest form of self-interaction is a so-called mass term.
• An interaction term links two different fields together. This means that if you have disturbances in two different particle fields, you either need to put in energy if they're near each other; or you get more energy out. So simply, when particles that interact approach each other, they are pulled towards each other, or away from each other. (The situation is usually more complicated than this, but this will do as a description!)

Now - in the Higgs mechanism - technical constraints mean that we're not allowed to just put the self-interaction term (for the field that we want to give mass to) straight into the Lagrangian. (And indeed that we don't want to do this.) So instead, we do the only other possible thing: we introduce an interaction term with another field, the Higgs field. But you can't have an interaction with a completely empty field, and having random Higgs particles bouncing around would not produce very even results for the mass.

This means that we want to choose the Higgs part of the Lagrangian so that the field isn't simply 0 in its default state, or ground state.

But how can we shift the field to be something away from zero? In particular, we need to break the symmetry so that the lowest energy state isn't at zero, but a little way away.

The only thing we are still free to change (without introducing more fields) is the self-interaction of the Higgs field. But we know what a potential looks like that breaks a symmetry like this: we choose it so it slopes downwards away from the symmetric point 0 - then, so that it settles down somewhere else, we make it curve up again a little way away. The classic example of this is called the 'Mexican hat' potential. If you want to see an example, look at the graph of 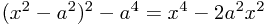- this is smallest when .

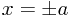Notice that the plus/minus ambiguity shows the broken symmetry if you slide to the bottom of the graph. In fact, fields are typically complex numbers, so there's actually a whole circle of low-energy states around 0 where 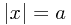; at a distance of a from 0.

And now we're essentially done! We've made the Higgs field 'stick up' a bit everywhere, and as a result the interaction terms mean that there's energy associated with ripples anywhere in the other matter fields - and this appears exactly as a mass term in the Lagrangian when the Higgs field is left in its natural state. Perfect!

What about the Higgs particle in this description? Notice that there is a whole circle of values in which the Higgs field can vary freely at each point in space. (Careful - the circle isn't in our space, it's completely abstract.) This freedom allows particles to travel through the Higgs field - you can get 'ripples' where the point on the circle occupied swings around as you follow the particle.

So when was the symmetry actually 'broken' historically? Well, in the early universe, there was lots of energy around, and the Higgs field didn't notice the little bump near the origin, since only high energy points are relevant most of the time. At this time, the interactions and energies due to mass were also fairly negligible - everything behaved like it was free and nearly massless. But then the universe expanded - as energy got more spread out and the universe cooled down, the field settled down into the circular channel around the lump in the middle.

The Mathematics

[more to come]

You could try The Unapologetic Mathematician's four-part series on the Higgs Mechanism.

Spontaneous Symmetry Breaking

The phenomenon underlying the Higgs mechanism - from intuition and mathematics

Return to top