A-level Physics has many flaws, but for me one of the worst aspects of my WJEC course was the section on particle physics, and particularly the explanation of Feynman diagrams given. The diagrams are usually used to explain processes of change like radioactive decay (showing a neutron/down quark decaying into an electron, proton/up quark and an antineutrino, as in beta decay, for example) but actually attempt to explain all particle interactions, including forces. The idea there is that all forces can actually be explained entirely in terms of particle [fields], or "by the exchange of virtual particles", using no action at a distance principles.

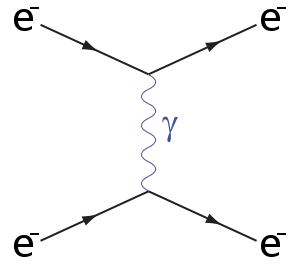
People usually talk about the process shown (technically the tree-level - specifically t-channel - case of Møller scattering) as being a pair of electrons 'exchanging a virtual photon'. This sort of explanation is very helpful for remembering and interpreting Feynman diagrams... once you already know what it means. The problem is that without some understanding of what they really mean, they contain lots of subtly confusing features.

• If these particles are point-like, how can the photon ever 'hit' the other electron?
• If an electron is constantly emitting photons "just in case" there's another one nearby, where does the energy come from? Where does the photon go if it doesn't find one?
• Which way does the photon go?
• How can a photon be 'virtual' and not 'physical'?

All these questions arise from assigning physical interpretations to the diagram, a very natural thing to do - indeed the diagram is deliberately constructed to be suggestive, partly because it's very natural once you derive the corresponding mathematics, and partly because it makes remembering the answer much easier. The key point here is that the diagrams are mathematically motivated, then physically (a bit dubiously perhaps) interpreted, not the other way round.

Where Feynman diagrams come from

Instead of messing about in the shallow end, we're going to take a jetski out onto the ocean to have a look down at the real depths of the subject we're interested in. (Metaphorically. We don't really need a jetski.)

The basic idea you build this sort of QFT (Quantum Field Theory) out of is a very simple picture, in which:

1. You look at the system and see some identifiable particles in some well-defined state.
2. You wait for a bit, and maybe something interesting happens.
3. You look again, and see what you recognize.

Schematically, you might draw two electrons going into a big blob, and then two electrons coming out again. Simple enough. We need to find a way of describing what goes on in the blob - in particular (since this is a quantum theory) we would like to know the probability that the electrons come out in some particular way, given they go in in some particular way.

But the first problems don't actually arise in the blob in the middle - conceptually, things are actually quite tricky in the first step. Why? Because even 'fundamental particles' are not fundamental! What do I mean by this?

The analogy here is actually fairly straightforward. In quantum field theory, you derive the existence of particles from the equations of a field. The rough way to visualize this is to imagine taking a 2D slice out of the 3D (spatial) world, and then imagining a fairly flat sea sitting more or less level on your slice. (So forwards and sideways are your usual directions, and you've hidden the vertical direction to replace it with somewhere you can draw a graph.) Then what one finds out is that ripples in this sea look and behave just like particles.

Aside: This naturally explains the so-called indistinguishability of particles at an intuitive level. To quote David Tong [ref]:

... two electrons are identical in every way, regardless of where they came from and what they've been through. The same is true of every other fundamental particle. Let me illustrate this through a rather prosaic story. Suppose we capture a proton from a cosmic ray which we identify as coming from a supernova lying 8 billion lightyears away. We compare this proton with one freshly minted in a particle accelerator here on Earth. And the two are exactly the same! How is this possible? Why aren't there errors in proton production? How can two objects, manufactured so far apart in space and time, be identical in all respects? One explanation that might be offered is that there's a sea of proton "stuff" filling the universe and when we make a proton we somehow dip our hand into this stuff and from it mould a proton. Then it’s not surprising that protons produced in different parts of the universe are identical: they're made of the same stuff. It turns out that this is roughly what happens. The "stuff" is the proton field or, if you look closely enough, the quark field.

It turns out there's some subtlety in defining exactly what you mean by the initial state as a result. (There are increasingly weird results as one investigates in more detail, like the Unruh effect in which different observers observe different numbers of particles, which mean particles are really not very fundamental.) But we'll skim over this, and just imagine some clumps of ripples far away from each other. Similarly, in the last stage, we'll look for some distinctive patterns of ripples moving away from each other again.

Important point: These ripples are not just like wavefunctions for single particles in normal quantum mechanics. You can still have a quantum superposition of different sorts of ripple - so a real 'wavefunction', or state, tells you what the probability is of the field having all different possible ripples. The ripples themselves are fairly classical.

So now we have to have a stab at understanding the big amorphous blob we've left in the middle of our problem. This is where the hard work in the theory of QFT comes.

The first thing to realize is that our interpretation of fields as fundamental has should change how we think of interactions completely, compared to our classical intuition. In particular, two related notions become obviously wrong:

• The idea that what we observe as particles are point-like things bouncing around.
• The clear interpretation of everything in the theory as a particle.

So imagine that you are sitting by a beach, with nice regular waves coming into shore - a beam of photons, perhaps. Then someone pushes a boat into the water from the beach, and a new bunch of waves are propelled out into the sea. They pass through each other, making complicated new shapes, and in fact (though it's usually very inconspicuous) interacting with each other, so that they emerged changed. The complicated shapes in the middle do not look like regular waves, but clearly are intuitively "made up" of nice regular ripples. That is the picture of particles we are aiming for.

Just as the main thing you see in the water is the superposition of the original pair of waves, mostly particles simply pass through each other and emerge unchanged. However, the ripples are not completely independent, and in the complicated mess in the middle, things can happen which change the outgoing waves. In the quantum setting, this can be very drastic, corresponding to completely different particle types.

To understand how a physical theory goes from some basic principles to predicting the probabilities that various things come out (at various angles, with various speeds, ...), we need to come to some understanding of this mess in the middle, as we said above. The idea of perturbative QFT is to view the importance of the interaction between these ripples as being some small parameter in the theory, and to divide the different sorts of mess which can happen up into classes which depend on how much interaction would be needed to make them happen - then we only need to worry about the ones with very little interaction, since we know the interaction is a small effect, so things with lots and lots of interactions are less important. (Mathematically, they are suppressed by higher powers of the coupling constant, which is what measures the interaction strength.)

Let's say that again in a simpler physical analogy: suppose you have two structures built out of tiny balls fixed (by magic) in a nice regular cubic array. The balls are much smaller than the space between them, so the structures are mostly empty space. Now you throw them at each other. Most of the time, they'll pass straight through each other. Sometimes, the balls will line up, and the structures will bounce off each other. Sometimes, the balls will line up again, and there will be a second bounce. And so on. The small parameter here - the size of the balls divided by the space between the balls - allows us to think about the ways the structure comes off incrementally. Firstly, we just calculate the angles they come out at if there is no interaction; then, we look at the 'first-order' effect of one bounce; next, the 'second-order' two-bounce effect. And so on, caring less and less about the things we describe as we go down.

This is what we do in the physics - ignoring the boring no-interaction case, we look primarily at 'tree-level' effects, like that shown in the opening diagram, which correspond to the minimum number of field interactions. In that diagram, there are two vertices, each with an electron in, an electron out and a photon. All this means is that we look for simpler classes of the usually messy ripples where there are only two photon field-electron field interactions (the smallest number if we want something interesting to happen, but no leftover photons). These are much less chaotic than the general interactions, but are by far the most important!

Formally, we are thinking of ripples as being complicated superpositions (mixtures) of simple, regular waves - particles of definite momentum - and then working out the effect of each individual simple ripple, then adding them all back together again. So the diagram is just describing the sorts of ripples we are supposed to add up for one term. It is not claiming that there is a moment where one electron emits a photon, and another where that photon is absorbed. Instead, it is saying that to work out how a pair of electron push each other away, one needs to add up lots of possible ripples that could occur ("invisibly" from the point of view of an outsider) with their relative probabilities, the most important of which can be made out of a single photon-like ripple.

There are two things buried in there:

• I say photon-like ripple because in general these ripples, or 'virtual particles', are not constrained to be exactly like the real versions of the particle. The particular oddness is that virtual particles can be off-shell - this means that, whilst the normal ripples of particles have a relationship between their energy (rippliness-in-time) and momentum (rippliness-in-space) determined by their mass, these components waves can have arbitrary energy and momentum (or putting these together, an arbitrary 4-momentum). This is not surprising, really - free particles have to be (relatively) long-lived, stable things which can propagate and stay the same, whereas arbitrary messy ripples could be much more complicated.
• What do I mean when I say this happens "invisibly"? In the quantum world, nothing is definite; instead, many different possibilities evolve alongside each other; when we make a measurement, we usually observe only a single outcome, but this is a complicated effect due to the fact we are much larger than the systems we are observing, so the entanglement is not obvious. The point is, however, that the mess of ripples is not observed, only the incoming and outgoing particles. Therefore, we have to think about (and add up the effects from) all possible 'things that could happen in between'. This explains the question raised above: "If an electron is constantly emitting photons just in case there's another one nearby, where does the energy come from? Where does the photon go if it doesn't find one?" Really, this diagram only arises to be summed over when there are two electrons! You cannot have an effect due to two incoming free electrons when there is only one.
  Of course, in reality there is all sorts of activity around 'free' particles, and even in the vacuum, but it doesn't look like the drawing above! It has only two, or zero, external legs.

[Mention the cluster expansion in Mayer f-functions.]

...

• See also: Prof. Matt Strassler's blog.

Feynman Diagrams & Virtual Particles

Explaining the real meaning - physical and mathematical - of Feynman diagrams and the 'virtual particles' they contain

Return to top