Representation Theory and Symmetries
Symmetries: Why Physicists Care
Classification is key to science in many ways; the classification of particles according to various properties - spin, mass, charge, ... - is one of the key concepts in physics. But why should such a classification exist and be useful, and how can we understand the one we see?
The key idea is to link these classifications with the concept of a symmetry. One can use Noether's theorem to understand how a symmetry gives rise to a conserved quantity; in contrast, one uses representation theory to understand how expected symmetries of the real world can be manifested by particles. The former is a very direct way to obtain expressions for conserved quantities corresponding to the properties above; the latter gives a fundamental insight into what is happening for each individual particle species, and is needed to correctly, say, obtain the possible spins of particles in our spacetime.
What is a symmetry?
We'll suppose our theory is defined by a bunch of fields (each of which will usually correspond to either one particle, or some fairly small number of related particles) which we shall lump together symbolically into the vector 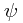 , and a Lagrangian density
, and a Lagrangian density 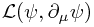 . We emphasize 'density' here to clarify that the Lagrangian is something different -
. We emphasize 'density' here to clarify that the Lagrangian is something different - 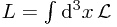 . Of course, if you are familiar with the principles of special (or general) relativity, you might be a bit upset at the use of the integral over space only, since that is not covariant. In that case, you would be more happy with the definition of the action S, a functional depending on the particular set of (classical) fields given:
. Of course, if you are familiar with the principles of special (or general) relativity, you might be a bit upset at the use of the integral over space only, since that is not covariant. In that case, you would be more happy with the definition of the action S, a functional depending on the particular set of (classical) fields given:
![S[\psi] = \int \mathrm{d}t \, L = \int \mathrm{d}^4 x\,\mathcal{L} S[\psi] = \int \mathrm{d}t \, L = \int \mathrm{d}^4 x\,\mathcal{L}](/_static/latex/f71303390d4687d8fead59fe490c6a61.gif)
Now we can define a symmetry straightforwardly: it is a map taking the function 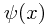 to a new function
to a new function ![\psi'(x) = \mathcal{F}[\psi] (x) \psi'(x) = \mathcal{F}[\psi] (x)](/_static/latex/2f26be9338a18927870756894b8e2685.gif) where the curly F represents the symmetry, which obeys the requirement
where the curly F represents the symmetry, which obeys the requirement
![S\left[\mathcal{F}[\psi]\right] = S[\psi'] = S[\psi] S\left[\mathcal{F}[\psi]\right] = S[\psi'] = S[\psi]](/_static/latex/e352c1f76dc3bdcf66443a11eaccaef7.gif)
for all fields 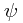 . Formally, such an
. Formally, such an 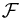 is a symmetry of the action.
is a symmetry of the action.
Note: If you're unhappy with the notion of a Lagrangian... you need to become happy with it! If you prefer, though, conceptually you can just think of something more like the Hamiltonian, or the energy of the system, in place of the Lagrangian. As for a concrete example, a massless scalar field would classically be a scalar function 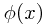 with Lagrangian density
with Lagrangian density 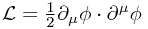 (in the +--- sign convention beloved of most particle physicists).
(in the +--- sign convention beloved of most particle physicists).
Examples: One might define ![\psi'(x) = \mathcal{F}_a[\psi] (x) = \psi(x + a) \psi'(x) = \mathcal{F}_a[\psi] (x) = \psi(x + a)](/_static/latex/9edca0bacc5ba790623e6a42c9c98bb9.gif) for some constant vector
for some constant vector 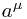 . Then the symmetry is called a translational symmetry. This is a symmetry of any complete flat-space system which treats all points equally. Note that this is (if I understand the terminology correctly, though I have never cared to try!) an active transformation, because we are currently thinking of a prescription
. Then the symmetry is called a translational symmetry. This is a symmetry of any complete flat-space system which treats all points equally. Note that this is (if I understand the terminology correctly, though I have never cared to try!) an active transformation, because we are currently thinking of a prescription 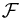 which takes one state
which takes one state 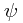 and gives us a new one,
and gives us a new one, 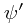 defined on the same space. However, we are clearly free to think of this differently, and think of the related passive transformation, in which we actually just change the coordinate system, so that
defined on the same space. However, we are clearly free to think of this differently, and think of the related passive transformation, in which we actually just change the coordinate system, so that 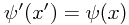 where
where 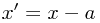 , and the two functions
, and the two functions 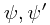 are the same function, evaluated in different coordinate systems.
are the same function, evaluated in different coordinate systems.
This particular alternative view does not hold for different symmetries, however; it might be that ![\psi'(x) = \mathcal{F}_C[\psi] (x) = \psi(x) + C \psi'(x) = \mathcal{F}_C[\psi] (x) = \psi(x) + C](/_static/latex/20a0ac2de53e5f3a9552fce49e7e103a.gif) is a symmetry for some constant number C, as for the free massless scalar field, for example. This could be a very simple gauge symmetry, and cannot be achieved by a change of coordinate. For this reason, I prefer to think in terms of the 'active' viewpoint, where a symmetry takes your old field and gives you a new one. Note, however, that gauge transformations (relating physically equivalent states) are very different to symmetries arising from coordinate transformations. [Mention the Coleman-Mandula theorem and supersymmetry.]
is a symmetry for some constant number C, as for the free massless scalar field, for example. This could be a very simple gauge symmetry, and cannot be achieved by a change of coordinate. For this reason, I prefer to think in terms of the 'active' viewpoint, where a symmetry takes your old field and gives you a new one. Note, however, that gauge transformations (relating physically equivalent states) are very different to symmetries arising from coordinate transformations. [Mention the Coleman-Mandula theorem and supersymmetry.]
What does this mean?
A symmetry of the action should correspond to a symmetry observed by someone conducting experiments. This is because (most obviously via Feynman path integrals) the action alone determines the physical rules obeyed by the system.
As mentioned above, Noether's theorem now gives an expression for a conserved current, with the property that the spatial integral of the 0 component is constant in time classically; in the quantum context, one finds an integral operator commuting with the Hamiltonian - thus one can simultaneously diagonalize both, and then the value of the integral operator is constant for an eigenbasis element. Instead, let us consider the actual behaviour of classical solutions under these transformations.
Note: A natural question to ask is "Why do we focus on classical solutions?" The most useful answer is to consider the procedure of quantization; for example, in canonical quantization of a free field, one expands the field operator in terms of a basis of classical solutions multiplied by related creation/annihilation operators, each of which corresponds to a particular excitation, and ultimately particle, one hopes. Thus classifying classical solutions nicely should correspond to classifying particles nicely.
The key assumption we will use in our classification is that the free particle theory, with linear equations of motion, is a good approximation to our theory, in some sense; most naïvely, one wants non-linear terms to have small coefficients. (Lots of subtleties come in - for example, renormalization means that these other terms can effectively correct the other terms non-trivially.) This is because we want to think only about these simple free field solutions.
Reversing the logic
We now want to understand not how nice symmetries of special Lagrangian densities lead to nice observable symmetries, but what the nature of particles must be in order to respect the symmetries inherent in three-dimensional space.
What do I mean? Let us assume that, to conform with our physical expectations, a system is translationally symmetric in the sense defined above. Then we expect that each ![\mathcal{F}_a[\psi] (x) = \psi(x + a) \mathcal{F}_a[\psi] (x) = \psi(x + a)](/_static/latex/38b7e7b884f53bec5f510877042cb9df.gif) is a symmetry of the system, whatever the unknown
is a symmetry of the system, whatever the unknown 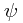 are. The key point here is that, supposing we have some basis for the classical solutions - this being a linear space, crucially - the right-hand side lies within the same space.
are. The key point here is that, supposing we have some basis for the classical solutions - this being a linear space, crucially - the right-hand side lies within the same space.
Now suppose that we could diagonalize this operator 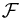 for all a - note that all the
for all a - note that all the ![\mathcal{F}_a[\psi] \mathcal{F}_a[\psi]](/_static/latex/ca2dc5d17d2479c4e762e84bfc16c0ce.gif) obviously commute, so this is reasonable. What do I mean by this? I want to find a collection of functions
obviously commute, so this is reasonable. What do I mean by this? I want to find a collection of functions 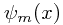 for some label m with the property that
for some label m with the property that
![\mathcal{F}_a[\psi_m] (x) = \psi_m(x + a) = f_m(a)\psi_m(x) \mathcal{F}_a[\psi_m] (x) = \psi_m(x + a) = f_m(a)\psi_m(x)](/_static/latex/3ce53a23b6a94a9a8f9f64df3d7a25ee.gif)
for some eigenvalues 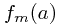 . In general,
. In general, 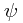 represents a column vector of fields, and we will allow the
represents a column vector of fields, and we will allow the 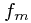 to be matrices in this case. Were we to find such a 'nice' basis, we can use our knowledge of the behaviour of transformations to deduce information about the
to be matrices in this case. Were we to find such a 'nice' basis, we can use our knowledge of the behaviour of transformations to deduce information about the 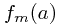 matrices.
matrices.
We know that composing two translations is just the same as doing both together: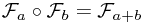 . This means that
. This means that 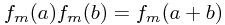 - this is quite a restriction on the possible ways that the f matrices can depend on the translation vector! In fact, if we only had a single field, then we could deduce (take logs) that
- this is quite a restriction on the possible ways that the f matrices can depend on the translation vector! In fact, if we only had a single field, then we could deduce (take logs) that 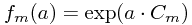 for some
for some 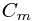 . (We could drop the 'for all a' bit above, and just consider translations by a. However, we would then deduce that it worked for all integer multiples of a, which is less strong - see below.)
. (We could drop the 'for all a' bit above, and just consider translations by a. However, we would then deduce that it worked for all integer multiples of a, which is less strong - see below.)
What can the 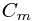 be? Remembering the
be? Remembering the 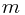 labels are arbitrary, we note that the dependence on
labels are arbitrary, we note that the dependence on 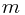 isn't interesting. If we assume that the action is quadratic in the fields, though, we note that there is no way
isn't interesting. If we assume that the action is quadratic in the fields, though, we note that there is no way 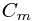 has non-zero real part, as this would lead to unbounded contributions to some carefully chosen integrals, violating the condition that this is a symmetry. Hence without loss of generality,
has non-zero real part, as this would lead to unbounded contributions to some carefully chosen integrals, violating the condition that this is a symmetry. Hence without loss of generality, 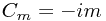 , and
, and 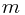 is essentially the momentum of the corresponding
is essentially the momentum of the corresponding 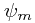 . (See the next section for clarity.)
. (See the next section for clarity.)
This is a bit unsatisfactory; we've posited the existence of some magical eigenbasis solving infinitely many different eigenvalue problems (the 'for all a' bit above) even if the terms did commute, and then dismissed the multi-field case. We will attempt to improve the former case first, and then see below how representation theory answers questions like that arising in arbitrary dimensions.
Infinitesimal approach
We definitely expect arbitrarily small translations to be symmetries of the system. What form do these take?
![\mathcal{F}_{a \mathrm{d}u}[\psi] (x) = \psi(x + a \mathrm{d}u) = \psi(x) + a^\mu \partial_\mu \psi(x) \mathrm{d}u + \mathcal{O}(\mathrm{d}u^2) \mathcal{F}_{a \mathrm{d}u}[\psi] (x) = \psi(x + a \mathrm{d}u) = \psi(x) + a^\mu \partial_\mu \psi(x) \mathrm{d}u + \mathcal{O}(\mathrm{d}u^2)](/_static/latex/4197161664f4aff7ac582d600f6a1166.gif)
Hence, dropping second order terms, we have 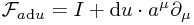 which is a nice local operator. Suppose we diagonalize this operator for some a. Then we have
which is a nice local operator. Suppose we diagonalize this operator for some a. Then we have
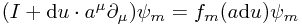
or, separating out 0th and 1st order terms, 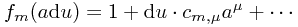 for some
for some 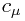 such that
such that
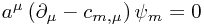
Now note that if we solve the eigenvalue problem for just one such a, we obtain a solution for all multiples of a. Hence focusing on just one direction at a time, say a coordinate direction, we note that diagonalizing four commuting operators is sufficient to diagonalize all infinitesimal transformations.
Now we are done! In the 1-field case, the 4-vector 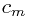 characterizes each solution, and can be seen to give the momentum - we have
characterizes each solution, and can be seen to give the momentum - we have 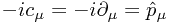 .
.
Outlook: Rotations and spin
Now we have seen how, in a very simple case, we can obtain a way of characterizing a basis of particle states using a symmetry. The key idea was looking for a basis which was transformed in a simple local way - essentially an eigenbasis of the symmetry - and investigating the behaviour of the 'eigenvalues', which can in general be constant matrices, under composition of symmetries. We have seen this only in a very simple case.
A much more rich topic is that associated with rotations. (In the following brief section, we will imply we are working with SO(3), but in fact - as outlined elsewhere on the site, one should in fact work with SU(2), as we will do in the following section.) Here, we have
![\mathcal{F}_\Omega[\psi] (x) = \psi(\Omega x) \mathcal{F}_\Omega[\psi] (x) = \psi(\Omega x)](/_static/latex/37d4bb1768a3355b85bfc08c1478a064.gif)
where 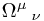 is a rotation matrix. Now we have composition being the non-abelian matrix multiplication of the
is a rotation matrix. Now we have composition being the non-abelian matrix multiplication of the 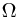 matrices. This means, amongst other things, that the big 1D simplifications of the above case cannot work except in the most trivial case. Why? Suppose
matrices. This means, amongst other things, that the big 1D simplifications of the above case cannot work except in the most trivial case. Why? Suppose 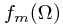 is just a number, not a matrix. Then we have
is just a number, not a matrix. Then we have
![f_m\left(\Omega_1\Omega_2\right)-f_m\left(\Omega_2\Omega_1\right) = \left[f_m(\Omega_1), f_m(\Omega_2)\right] = 0 f_m\left(\Omega_1\Omega_2\right)-f_m\left(\Omega_2\Omega_1\right) = \left[f_m(\Omega_1), f_m(\Omega_2)\right] = 0](/_static/latex/bdc75f94bf709fa30385d3d246d44cc6.gif)
but it is easy to show (a good exercise, involving choosing one matrix given the other is a rotation by θ about some axis, and deducing that rotating by θ has the same f as rotating by -θ, and since composition gives the identity, 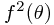 = 1) that this means
= 1) that this means 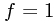 is the only non-zero solution. (You might like to try this infinitesimally too!)
is the only non-zero solution. (You might like to try this infinitesimally too!)
So we need to venture into understanding what possible interesting forms the matrix 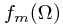 can take whilst preserving
can take whilst preserving
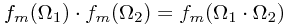
This leads us to...
Representation Theory
Let us (in the light of the note above, which referred to this other article for justification) think about what possible matrices could obey
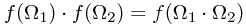
and also, obviously,
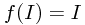
for 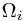 in the group SU(2) of special unitary matrices, and I standing for two (in general of different size!) identity matrices. To get a grip on this, we make some definitions...
in the group SU(2) of special unitary matrices, and I standing for two (in general of different size!) identity matrices. To get a grip on this, we make some definitions...